Ass Wr Wb
Jika ingin membaca lebih lanjut perihal POSITIVISME, silahkan konek berikut:
KANT’S ACCOUNT
OF SCIENCE
By Marsigit, Yogyakarta State University
Email: marsigitina@yahoo.com
It was elaborated in Stanford Encyclopedia
of
Jumat, 30 November 2012
Rabu, 28 November 2012
SOAL DAN PEMBAHASAN UN MATEMATIKA SD 2011
Soal Ujian Nasional SD : Telah saya peroleh Soal dan Pembahasan matematika un 2011 SD. Kamu dapat langsung mendownloadnya dengan cara mengklik link berikut ini. sekali klik langsung download!
SOAL DAN PEMBAHASAN UN MATEMATIKA SMP TAHUN 2012
Siswa SMP juga harus dipersiapkan dengan matang dalam menghadapi ujian nasional 2013. terutama pada mata pelajaran matematika yang menjadi momok mereka. Soal dan pembahasan ujian nasional matematika smp 2012, semoga bermanfaat. klik saja pada link di bawah ini untuk mendownloadnya!!
SOAL DAN PEMBAHASAN UN MATEMATIKA SMA 2012 IPS
Saya juga berika soal dan pembahasan Ujian Nasional Matematika tahun 2012 untuk program studi IPS. Silahkan download dan pelajari serta pahami setiap penyelesaian soal. Semoga nanti membantu dalam mempersiapkan menghadapi Ujian Nasional 2013 khususnya pada mata pelajaran matematika. oke...tampa memperbanjang lebar lagi, ini dia downloadnya!
SOAL DAN PEMBAHASAN UN MATEMATIKA SMA 2012 IPA
Berikut kami lampirkan Soal dan Pembahasan Ujian Nasional Matematika SMA 2012, semoga dapat menjadi bahan latihan bagi para siswa dalam menghadapi ujian nasional 2013 beberapa saat lagi. langsung saja download dan langsung sebarkan kepada teman-teman kamu semua.
Selasa, 27 November 2012
Workshop for a Living
I plan the vast majority of my lessons now with a workshop structure. It's become an integral part of how I think about lessons, much as Launch-Explore-Summarize used to. Or the "keep the students busy the whole time" strategy that came before that. (I can keep going here...)
What do you want preservice teachers to know about lesson planning, and when do you want them to know it? The Math for Secondary course that I'm teaching this semester is the first math ed course that our students take. Then we get them for a Math for Middle School course, and then we got to observe them in the field and have a weekly seminar during the first semester of their internship. Just recently we've added more time with them during student teaching, their 2nd semester of internship. We're trying to get away from doing lots of lesson planning for imaginary students. But when they start their internship, lesson planning is what they feel most nervous about. (Survey says.)
Recently I had a class with the objective to get these ultra-novice teachers started on thinking about lesson structure. There's so many ways to consider...
Students were working from a section in Statistics in Action from Key Curriculum Press, and tried every model except 3 acts. (Makes sense given their resource.) Why ITIP...?
So why workshop for me? An article from a bunch of us that we've been working on summarizes the workshop with this table:
Despite the fact that we all implement the workshop differently, these are the commonalities. So maybe just a word about the phases and why I feel they're necessary.
Objective: what? That's not in the table! But it's this structure that has helped me be clearer with myself about what it is I want students to get out of a lesson, and clearer in communicating it to students as well. I used to like lessons to be like a surprise, but that is a cheap way to get suspense. If you can tell the objective up front, and still generate the mystery... that's good teaching. I'm working on it.
Schema Activation: part for the students to give them something on which to build new understanding, part for me as pre-assessment, this has been very helpful. One of the best things I have to share as a math teacher is my connected view of mathematics. How does this relate to what we've done before, what ideas do you want to refresh before tackling new material, or what questions do you have about previous times you've seen this that you might not even know you had. Why does that work? Why does it matter? Is there another way to do it?
Focus: this phase has helped let me back into the classroom. When I became convinced of the centrality of student activity, I went extreme. I tried to minimize what I shared to things that just got students started on their activity. It was an improvement, but it left a lot of my students without the support that they needed. I see this phase as part equipping for the activity, part selling of the purpose, and part testimonial as I share some of my experience or thinking. Activities that students used to struggle with nonconstructively have become high impact learning opportunities with this phase, and frustration has reduced.
Activity: always the heart and soul of the lesson. Rich tasks on important mathematics. Often with some kind of choice built in. Usually cooperative, as I value the power of that mathematically and for learning. This phase can have none or many places where we come back together as a whole class. Sometimes to share what groups are doing, sometimes to address a common stumbling block, sometimes to just refocus attention on the task at hand.
Reflection: but activity is not enough. The research that showed differences in retention depended more on consolidation than on activity vs lecture really effected me. Whereas I used to just want to summarize - and that is still important to me - now I want the students to spend time thinking about what they did, what was important, what was new and to get time to record that. It has helped me with student retention, formative assessment, and re-emphasizing the objective. My most common form here is to have students write a bit about what they want to remember, what seemed important or what comes next, and then share with their group what they wrote. Excellent eavesdropping opportunity. It's been hard to cut off an engaging activity for this, but it is always worth it.
So that's why workshop is good for me. I shared with the novice teachers that I used to want them all to try to teach, but now I hope for two things:
What instructional structure(s) do you use? Why?
Postscript: Dave, Esther and I are presenting on this tomorrow. We probably won't use the slides, but they make a good resource.
What do you want preservice teachers to know about lesson planning, and when do you want them to know it? The Math for Secondary course that I'm teaching this semester is the first math ed course that our students take. Then we get them for a Math for Middle School course, and then we got to observe them in the field and have a weekly seminar during the first semester of their internship. Just recently we've added more time with them during student teaching, their 2nd semester of internship. We're trying to get away from doing lots of lesson planning for imaginary students. But when they start their internship, lesson planning is what they feel most nervous about. (Survey says.)
Recently I had a class with the objective to get these ultra-novice teachers started on thinking about lesson structure. There's so many ways to consider...
Students were working from a section in Statistics in Action from Key Curriculum Press, and tried every model except 3 acts. (Makes sense given their resource.) Why ITIP...?
So why workshop for me? An article from a bunch of us that we've been working on summarizes the workshop with this table:
Despite the fact that we all implement the workshop differently, these are the commonalities. So maybe just a word about the phases and why I feel they're necessary.
Objective: what? That's not in the table! But it's this structure that has helped me be clearer with myself about what it is I want students to get out of a lesson, and clearer in communicating it to students as well. I used to like lessons to be like a surprise, but that is a cheap way to get suspense. If you can tell the objective up front, and still generate the mystery... that's good teaching. I'm working on it.
Schema Activation: part for the students to give them something on which to build new understanding, part for me as pre-assessment, this has been very helpful. One of the best things I have to share as a math teacher is my connected view of mathematics. How does this relate to what we've done before, what ideas do you want to refresh before tackling new material, or what questions do you have about previous times you've seen this that you might not even know you had. Why does that work? Why does it matter? Is there another way to do it?
Focus: this phase has helped let me back into the classroom. When I became convinced of the centrality of student activity, I went extreme. I tried to minimize what I shared to things that just got students started on their activity. It was an improvement, but it left a lot of my students without the support that they needed. I see this phase as part equipping for the activity, part selling of the purpose, and part testimonial as I share some of my experience or thinking. Activities that students used to struggle with nonconstructively have become high impact learning opportunities with this phase, and frustration has reduced.
Activity: always the heart and soul of the lesson. Rich tasks on important mathematics. Often with some kind of choice built in. Usually cooperative, as I value the power of that mathematically and for learning. This phase can have none or many places where we come back together as a whole class. Sometimes to share what groups are doing, sometimes to address a common stumbling block, sometimes to just refocus attention on the task at hand.
 |
| Image by Duncan~ @ Flickr |
So that's why workshop is good for me. I shared with the novice teachers that I used to want them all to try to teach
- that they will teach intentionally, purposefully choosing a structure rather than relying on what's always been done.
- that they will evaluate by meaningful assessment of student understanding.
What instructional structure(s) do you use? Why?
Postscript: Dave, Esther and I are presenting on this tomorrow. We probably won't use the slides, but they make a good resource.
Mathematical tools – Part 2
Were it not for convoluted language, plenty of lawyers would be out of work. Educators, though, shouldn't be subjected to such torture.
William McCallum, one of CCSSI’s authors, wrote in the comments section of an article appearing on The Atlantic Magazine website, written by Barry Garelick, ``I agree with you that there is a lot of misreading of the standards out there in the field, and this is a problem.’’ Such arrogance. The real problem is that CCSSI is poorly written, not only substantively, but also in its lack of clarity.
7.G.2’s ``Focus on constructing triangles from three measures of angles or sides...‘’ is at best, ambiguous. Writing intelligible English is not the same as constructing logic gates, where the definition of ``or’’ invariably includes the possibility of both. The parallelism in the sentence implies you are given either 3 angles or 3 sides, but we suspect it’s supposed to mean the following: ``Focus on constructing triangles given various combinations of three angles and/or sides.’’
Read more »
William McCallum, one of CCSSI’s authors, wrote in the comments section of an article appearing on The Atlantic Magazine website, written by Barry Garelick, ``I agree with you that there is a lot of misreading of the standards out there in the field, and this is a problem.’’ Such arrogance. The real problem is that CCSSI is poorly written, not only substantively, but also in its lack of clarity.
7.G.2’s ``Focus on constructing triangles from three measures of angles or sides...‘’ is at best, ambiguous. Writing intelligible English is not the same as constructing logic gates, where the definition of ``or’’ invariably includes the possibility of both. The parallelism in the sentence implies you are given either 3 angles or 3 sides, but we suspect it’s supposed to mean the following: ``Focus on constructing triangles given various combinations of three angles and/or sides.’’
Pretty Petals
I was appreciating the geometrydaily:
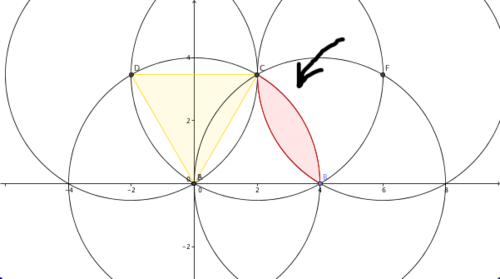
And got to noticing the always neat equliateral triangle proportions in the circle where the side length is the radius. So I have to fire up GeoGebra and start playing.#332 Totem – A new minimal geometric composition each day
Now I'm quite curious about those special lengths of the petals. Here's the sketch if you'd like to play with it: teacher's page (download) and student's page (applet).
Other GeoGebra inspired by Geometry Daily:
Senin, 26 November 2012
ICT പഠനം : പത്താംക്ലാസ് വര്ക്കുകള്
തിയറി ചോദ്യങ്ങള്ക്ക് ഉത്തരമെഴുതാന് ഇവ സഹായിക്കുമെന്ന് കരുതാം.
Click here for theory notes of Networking
ഇനി പ്രാക്ടിക്കല് പരിശീലനത്തെക്കുറിച്ചു പറയട്ടെ. ഏഴുപാഠഭാഗങ്ങളില് നിന്നും പ്രാക്ടിക്കല് ചോദ്യങ്ങള് പ്രതീക്ഷിക്കാം. ഇങ്ക് സ്ക്കേപ്പ്, സ്പ്രെഡ് ഷീറ്റ്, ക്യൂജിസ്, പൈത്തണ്, ടൂപ്പി 2D മാജിക്ക്, സ്റ്റെല്ലേറിയം, കെ ടെക് ലാബ്, ജിയോജിബ്ര എന്നീ സോഫ്റ്റ് വെയറുകളും വെബ് പേജ് നിര്മ്മാണവും (html , KampoZer) പരിശീലിപ്പിക്കണം. 20 വര്ക്ക് ഷീറ്റുകള് ഇതിനായി തയ്യാറാക്കിയിട്ടുണ്ട്. ഇവ ചോദ്യങ്ങള് മാത്രമാണ്. പ്രിന്റെടുത്ത് ഓരോ സിസ്റ്റത്തിനും ഒരു കോപ്പിവീതം വെച്ച് കുട്ടികളെ പരിശീലിപ്പിക്കാന് കഴിഞ്ഞാല് വളരെ ഭംഗിയായി പരീക്ഷ എഴുതുമെന്ന് ഉറപ്പുണ്ട്. മൂന്നു വര്ക്ക് ഷീറ്റുകള് താഴെ കൊടുത്തിരിക്കുന്നു. ബാക്കിയുള്ളവ തുടര്ന്നുള്ള പോസ്റ്റുകളില് പ്രതീക്ഷിക്കാം
Practice practical Work 1
Practice Practical Work 2
Practice Practical Work 3
