Like everyone else, I suppose, I have a need to express my creativity. To facilitate this I am coding a small programming language to create graphical art. Although, for me, Mathematica is -the- language to do that I want to have a language that kids of age 8 to 88 ( TinTin or Donald Duck readers ) could learn. By using it geometric transformations like rotations and translations are learned in a natural way.
The graphic like the one below, including the rotation, is an example what the language could create with a few lines, a Mathematica Kernel is required but will run in the background only.
To be continued.
Senin, 31 Oktober 2011
Minggu, 30 Oktober 2011
ഉബുണ്ടുവിലെ നെറ്റ് വര്‍ക്കിങ്ങ്
ഉപജില്ലാ കലോത്സവം ഡാറ്റാ എന്‍ട്രിക്കായി സ്ക്കൂള്‍ ലാബില്‍ നിരത്തി വച്ചിരിക്കുന്ന കമ്പ്യൂട്ടറുകള്‍. പ്രിന്റര്‍ കണക്ട് ചെയ്ത സിസ്റ്റത്തില്‍ കാര്യമായി വര്‍ക്കു ചെയ്തു കൊണ്ടിരിക്കുന്ന സഹപ്രവര്‍ത്തകന്‍. അദ്ദേഹത്തെ ശല്യപ്പെടുത്താതെ തന്നെ മറ്റേതെങ്കിലും സിസ്റ്റത്തില്‍ നിന്നും പ്രിന്റ് കൊടുക്കുന്നു. പ്രിന്ററില്‍ നിന്നും കൃത്യമായി പ്രിന്റ് ലഭിക്കുന്നു. ഇത്തരമൊരു വിദ്യ നമ്മുടെ വിദ്യാലയങ്ങളിലും പരീക്ഷിക്കേണ്ടേ? ഇക്കാര്യം പരിഹരിക്കുന്നതിന് നെറ്റ്‍വര്‍ക്കിങ്ങിനെക്കുറിച്ചുള്ള ഒരു പോസ്റ്റ് മാത്സ് ബ്ലോഗില്‍ പ്രസിദ്ധീകരിക്കണമെന്ന് പലരും ആവശ്യപ്പെടാന്‍ തുടങ്ങിയിട്ട് നാളേറെയായി. ഉപജില്ലാ കലോത്സവവും ശാസ്ത്രമേളയുമെല്ലാം അരങ്ങു തകര്‍ക്കുമ്പോള്‍ ഈ പോസ്റ്റിന് ഏറെ പ്രസക്തിയുണ്ടെന്ന് ഞങ്ങള്‍ കരുതുന്നു. നെറ്റ്വര്ക്ക് കേബിളുകള്‍ വലിച്ചിട്ടുണ്ടെങ്കില്‍ അത് കോണ്‍ഫിഗര്‍ ചെയ്യുന്നതിനുള്ള മാര്‍ഗമാണ് ഈ പോസ്റ്റില്‍ വിശദീകരിക്കുന്നത്. കൊല്ലം ജില്ലയിലെ അമൃത സംസ്കൃത ഹയര്‍സെക്കന്ററി സ്ക്കൂള്‍, പാരിപ്പളളിയില്‍ നിന്നുള്ള ബിനു സാറാണ് ഈ പോസ്റ്റ് നമ്മുടെ ആവശ്യപ്രകാരം തയ്യാറാക്കി അയച്ചു തന്നിരിക്കുന്നത്. എസ്.എസ്.എല്‍.സി എ ലിസ്റ്റ് ഡാറ്റാ എന്‍ട്രി സമയത്ത് സാങ്കേതിക രംഗത്തെ അദ്ദേഹത്തിന്റെ മികവ് നാം കാണുകയുണ്ടായതാണ്. ഈ പോസ്റ്റും ഏറെ ഗുണകരവും എന്നെന്നും ഉപകാരപ്പെടുന്നതുമാണ്. സ്ക്കൂളില്‍ ഒട്ടേറെ കമ്പ്യൂട്ടറുകളുണ്ടെങ്കിലും ഒന്നില്‍ മാത്രമേ ഇന്റര്നെറ്റ് ഫസിലിറ്റി ഉള്ളൂ എന്ന പ്രശ്നം ഒട്ടേറെ പേര് നേരിടുന്നുണ്ട്. അതൊഴിവാക്കാമെന്നു മാത്രമല്ല, പ്രാക്ടിക്കല്‍ പരീക്ഷയുടെ മാര്‍ക്ക് കോപ്പി ചെയ്യ്തെടുക്കാന്‍ പെന്‍ഡ്രൈവുമായി എല്ലാ സിസ്റ്റങ്ങളിലേക്കും ഓടി നടക്കേണ്ട അവസ്ഥ ഭാവിയിലെങ്കിലും നമുക്ക് ഒഴിവാക്കാന്‍ കഴിയും. അതെങ്ങനെയെന്ന് ചുവടെ വിശദീകരിച്ചിരിക്കുന്നു. ഒപ്പം ഏറ്റവും ഒടുവിലായി വിന്‍ഡോസ്-ഉബുണ്ടു ഫയല്‍ ഷെയറിങ്ങും സ്ക്കൂള്‍ ലാബിലെ മറ്റു കമ്പ്യൂട്ടറുകളില്‍ നടക്കുന്ന പ്രവര്‍ത്തനങ്ങള്‍ നമ്മുടെ കമ്പ്യൂട്ടറില്‍ കാണുന്നതിനുള്ള മാര്‍ഗവും ചേര്‍ത്തിരിക്കുന്നു.1. മോഡത്തില്‍ നിന്നും wired ആയി ഇന്റര്നെറ്റ് കണക്ഷന്‍ ലഭിക്കുന്നുണ്ടോയെന്ന് നോക്കുക. ഇന്റര്നെറ്റ് ലഭിക്കുന്നുണ്ടെങ്കില്‍ നെറ്റ് വര്‍ക്ക് ചെയ്യാം.
* (ലാപ്‌ടോപ്പാണെങ്കില്‍ നെറ്റ് വര്‍ക്ക് കണക്ഷന്റെ ഐക്കണില്‍ റൈറ്റ് ക്ലിക്ക് ചെയ്ത് Enable wirless ലെ ടിക് മാര്‍ക്ക് കളഞ്ഞ് വേണം പരീക്ഷിക്കാന്‍ )
** (ഇന്റര്നെറ്റ് കിട്ടുന്നില്ലെങ്കില്‍ നെറ്റ് വര്‍ക്ക് ഐക്കണില്‍ റൈറ്റ് ക്ലിക്ക് ചെയ്ത് Edit Connections എടുക്കുക. wired connection ന്റെ edit ല്‍ ക്ലിക്ക് ചെയ്ത് IPV4 settings ലെ method ല്‍ DHCP ആക്കിക്കൊടുക്കുക. wired ല്‍ ഉള്ളത് Delete ചെയ്ത് add ബട്ടണ്‍ വഴി പുതിയൊരു കണക്ഷനെടുത്ത് Edit വഴി മുകളിലെ വരിയില്‍ പറഞ്ഞ പോലെ ചെയ്യുക.)
(*** System - administration - users & Group എടുത്ത് എല്ലാ പെര്‍മിഷനും നല്‍കണം)
2. നെറ്റ് വര്‍ക്ക് ചെയ്യേണ്ട എല്ലാ സിസ്റ്റത്തിലും ഇതു പോലെ ചെയ്തതിനു ശേഷം എല്ലാം ഓഫ് ചെയ്ത് വെക്കുകയും തുടര്‍ന്ന് ഓരോന്നോരോന്നായി ഓണാക്കുകയും ചെയ്യുക. (ഓരോ സിസ്റ്റത്തിനും വ്യത്യസ്ത IP Address ലഭിക്കാനാണിത്) ഏത് സിസ്റ്റത്തിലാണോ offline software ഇന്‍സ്റ്റാള്‍ ചെയ്തിരിക്കുന്നത് അതാണ് സെര്‍വര്‍. അതിലെ നെറ്റ്വര്ക്ക് ഐക്കണില്‍ റൈറ്റ് ക്ലിക്ക് ചെയ്യുമ്പോള്‍ Connection Information ല്‍ അതിന്റെ IP Address നമുക്ക് കാണാനാകും. അത് ഓര്‍മ്മിച്ചു വെക്കണം.
3. അതിനു ശേഷം നെറ്റ് വര്‍ക്ക് ചെയ്തിരിക്കുന്ന സിസ്റ്റങ്ങളിലെ ബ്രൗസര്‍ തുറന്ന് സെര്‍വറിന്റെ അഡ്രസ് ബാറില്‍ ഐപി അഡ്രസ് നല്‍കി തുടര്‍ന്ന് സെര്‍വറിലെ local host എന്നു കഴിഞ്ഞു വന്നിരിക്കുന്ന ഭാഗം അതേ പടി ടൈപ്പ് ചെയ്യുക.
ഉദാ: സെര്‍വറിന്റെ IP Adress 192.168.1.3 ആണെങ്കില്‍ നെറ്റ് വര്‍ക്കില്‍ ഉള്ള അടുത്ത സിസ്റ്റത്തില്‍ ശാസ്ത്രമേള എന്റര്‍ ചെയ്യേണ്ടത് താഴെ പറയുന്ന പോലെ
http://192.168.1.3/sciencefair_subdistrict/index.php എന്നായിരിക്കും. ശാസ്ത്രമേളയ്ക്കും ഉപജില്ലയ്ക്കുമെല്ലാം സാധാരണഗതിയില്‍ ഇത്രയും മതി നെറ്റ് വര്‍ക്കിങ്ങ്.
ഇനി നമുക്ക് കാര്യഗൗരവത്തോടെ ഫയല്‍ ഷെയറിങ്ങും പ്രിന്റര്‍ ഷെയറിങ്ങുമെല്ലാം എപ്രകാരമാണെന്ന് നോക്കാം. Network ചെയ്തിട്ടുളള computer കളില്‍ operating system ത്തില്‍ ചെയ്യേണ്ട മാറ്റങ്ങള്‍ മുതല്‍ ഓരോ സ്റ്റെപ്പും കൃത്യമായി ചെയ്യുക.
Network IP Address set ചെയ്യാന്‍
System – Preferences – Network Connections. എന്ന option select ചെയ്യുക.
അതിനു ശേഷം വരുന്ന ജാലകത്തില്‍ Auto eth0 select ചെയ്ത് Edit click ചെയ്യുക
ഇപ്പോള്‍ തുറന്നു വരുന്ന 'Editing Auto eth0' എന്ന ജാലകത്തിലെ ‘IPv4 Settings’ tab select ചെയ്ത് method എന്ന option ല്‍ manual ആക്കുക. അതിനു ശേഷം Add ബട്ടനില്‍ click ചെയ്ത് IP address താഴെ പറയുന്ന രീതിയില്‍ set ചെയ്യുക.
Address : 192.168.0.1 ( ഒരോ കമ്പ്യൂട്ടറിനും വ്യത്യസ്ത Address നല്‍ക്കുക. Eg : 192.168.0.2, 192.168.0.3 etc)
Netmask : 255.255.255.0
Gateway : 192.168.1.1 ( Internet Modem IP address)
DNS servers: 192.168.1.1 ( Internet Modem IP address)
Apply ബട്ടണ്‍ അമര്‍ത്തുക. അതിനു ശേഷം Network restart ചെയ്യുക.
Network restart ചെയ്യാന്‍
Applications-Accessories-Terminalഎന്ന ക്രമത്തില്‍ ടെര്‍മിനല്‍ തുറന്ന്
sudo /etc/init.d/networking restart എന്ന് ടൈപ്പ് ചെയ്ത് Enter അടിക്കുക
മുകളില്‍ പറഞ്ഞിരിക്കുന്ന കാര്യങ്ങള്‍ network ചെയ്ത ഓരോ computer ലും അവര്‍ത്തിക്കുക. ഓരോ computerനും പ്രത്യേകം IP address നല്‍ക്കാന്‍ മറക്കരുത്.
Printer share ചെയ്യാന്‍
Printer connect ചെയ്തിട്ടുളള computer ല്‍ ചെയ്യേണ്ട പ്രവര്‍ത്തനങ്ങള്‍
System–Administration–Printing എന്ന option select ചെയ്യുക.
ഇപ്പോള്‍ computer ല്‍ add ചെയ്ത printer കാണാം.
ഇതില്‍ Server–Settings എന്ന option select ചെയ്യുക.അതിലെ എല്ലാ ഓപ്ഷനിലെയും check box click ചെയ്യുക. Ok ബട്ടണ്‍ അമര്‍ത്തുക.
Install ചെയ്ത printer ല്‍ right click ചെയ്ത് shared option select അണോ എന്ന് പരിശോധിക്കുക. Select അല്ലായെങ്കില്‍ select ചെയ്യുക.Network ചെയ്ത computer കളില്‍ ചെയ്യേണ്ട പ്രവര്‍ത്തനങ്ങള്‍
System–Administration–Printing എന്ന option select ചെയ്യുക.
ഇപ്പോള്‍ കിട്ടുന്ന printing എന്ന ജാലകത്തില്‍ add ബട്ടണ്‍ select ചെയ്യുക.
ഇപ്പോള്‍ കിട്ടുന്ന New printer ജാലകത്തില്‍ Select Device എന്ന option ല്‍ Network Printer select ചെയ്യുക.തുടര്‍ന്ന് വരുന്ന option നില്‍ Find Network Printer select ചെയ്യുക.
ഇപ്പോള്‍ കിട്ടുന്ന ജാലകത്തില്‍ Host എന്ന option ന് നേര്‍ക്ക് printer connect ചെയ്ത computer ന്റെ IP address type ചെയ്ത് Find ബട്ടണ്‍ അമര്‍ത്തുക.
കുറച്ച് സമയത്തിന് ശേഷം printer find ചെയ്ത് verify option കാണിക്കും.verify ബട്ടണ്‍ click ചെയ്ത് verify ചെയ്യുക.
അതിനു ശേഷം Forward ബട്ടണ്‍ അമര്‍ത്തുക.
Printer driver install ചെയ്തതിനു ശേഷം വരുന്ന ജാലകത്തില്‍ Apply ബട്ടണ്‍ അമര്‍ത്തുക.
ഇപ്പോള്‍ network printer add ആയി കഴിഞ്ഞു.
ഇതേ രീതിയില്‍ share ചെയ്ത windows printer നെ network printer ആയി add ചെയ്യാം
File Sharing ( Connect to sever)
Places–Connect to server എന്ന option select ചെയ്യുക.
ഇപ്പോള്‍ കിട്ടുന്ന ജാലകത്തില്‍ service type SSH select ചെയ്യുക.
Server എന്ന option ന് നേര്‍ക്ക് connect ചെയ്യാനുളള computer ന്റെ IP address type ചെയ്യുക. connect ബട്ടണ്‍ അമര്‍ത്തുക.
Connect ചെയ്യാനുളള computer ന്റെ user name ഉം password ഉം type ചെയ്ത് login ചെയ്യുക.
File sharing ( Windows & Linux) samba വഴി- Windows ഉം Linux ഉം തമ്മില്‍ file, printer തുടങ്ങിയവ share ചെയ്യാന്‍ ഉപയോഗിക്കുന്ന ഒരു free software ആണ് samba .
- Synaptic package manager വഴി computer ല്‍ samba install ചെയ്തിട്ടുണ്ടോ എന്ന് പരീശോധിക്കുക.
- ഇല്ലായെങ്കില്‍ internet connect ചെയ്ത computer കളില്‍ terminal ല്‍ sudo apt-get install samba smbfs എന്ന് type ചെയ്ത് enter അമര്‍ത്തുക
Terminal ല്‍ nautilus smb://IP address (file access ചെയ്യാനുളള computer ന്റെ IP address) type ചെയ്ത് enter അമര്‍ത്തുക
Eg : nautilus smb://192.168.0.1
ഇപ്പോള്‍ പുതിയൊരു nautilus ജാലകത്തില്‍ share ചെയ്ത windows file കള്‍ കാണാം.
windows ല്‍ നല്‍കിയിരിക്കുന്ന sharing option ന് അനുസരിച്ച് ഈ file കളെ മാറ്റം വരുത്താന്‍ സാധിക്കും.
UBUNTU – UBUNTU File sharing
Ubuntu വില്‍ folder ന് sharing permission നല്‍കുന്നതിന്
share ചെയ്യാനുളള folder ല്‍ right button അമര്‍ത്തി sharing option select ചെയ്യുക. ( sharing option ലഭിക്കണമെങ്കില്‍ computer ല്‍ samba install ചെയ്തിരിക്കണം) folder ന് അവശ്യമായ sharing option കള്‍ നല്‍കി create share button അമര്‍ത്തുക.
Terminal ല്‍ nautilus smb://ip address (file access ചെയ്യാനുളള computer ന്റെ IP address) type ചെയ്ത് enter അമര്‍ത്തുക
Eg : nautilus smb”//192.168.0.1
ഇപ്പോള്‍ പുതിയൊരു nautilus ജാലകത്തില്‍ share ചെയ്ത file കള്‍ കാണാം.
Remote Desktop
മറ്റ് computer കളുടെ Desktop കാണുന്നതിനും നിയന്ത്രിക്കുന്നതിനും സഹായിക്കുന്ന സങ്കേതമാണ് ' Remote Desktop'. ഇത് പ്രവര്‍ത്തനക്ഷമമാക്കുന്നതിന് രണ്ട് ഘട്ടങ്ങളുണ്ട്.
ഡെമോണ്‍സ്റ്റ്രേഷന്‍ നടത്തുന്ന computer ലെ മറ്റ് computer കള്‍ക്ക് കാണാന്‍ അനുവദിക്കല്‍
System–Preferences–Remote Desktop തിരഞ്ഞെടുക്കുക.
Allow other users to view your desktop ടിക്ക് ചെയ്യുക.
ഈ computer ല്‍ ചെയ്യുന്ന പ്രവര്‍ത്തനങ്ങള്‍ മറ്റ് computer കളില്‍ നിന്നും നിയന്ത്രിക്കുവാന്‍ അനുവാദം കൊടുക്കുന്നതിന് " Allow other users to control your Desktop" ടിക്ക് ചെയ്യുക.
Security option ല്‍ അവശ്യമായ മാറ്റങ്ങള്‍ വരുത്തുക.
ഡെമോണ്‍സ്റ്റ്രേഷന്‍ കാണേണ്ട computer ല്‍ " Remote Desktop “ ദൃശ്യമാക്കുന്നതിനുളള program പ്രവര്‍ത്തിപ്പിക്കല്‍
Terminal തുറന്ന് vncviewer IP address എന്ന് type ചെയ്ത് enter അമര്‍ത്തുക
Eg : vncviewer 192.168.0.3
പുതിയ ജാലകത്തില്‍ network ല്‍ ഉള്‍പ്പെട്ട , നിങ്ങള്‍ ആവശ്യപ്പെട്ട computer ന്റെ Desktop കാണാം.
(computer ല്‍ vncviewer install ചെയ്തിരിക്കണം)
Sabtu, 29 Oktober 2011
M381 - Challenge Exercise
In the Open University course Number Theory and Mathematical Logic the additional exercises sections of the workbooks are complemented with several 'challenge exercises'. This is one of them.
To be continued.
Let $n$ be an odd positive integer.
Prove that there are $\tau(n)$ ways of writing $n$ as a sum of consecutive positive integers.
For example, if $n=9$, $\tau(9)=3$ because $9$ has three divisors $1,3,9$ and the three sums are: $9$, $4+5$ and $2+3+4$.
To be continued.
INDONESIA MATHEMATICS COMPETITION 2011
Dalam rangka memeriahkan INDONESIA BOOK FAIR (IBF) 2011 dan sekaligus untuk meningkatkan kualitas belajar mengajar di bidang Matematika serta menciptakan semangat kompetisi di lingkungan siswa maupun guru/sekolah SD, SMP, dan SMA, maka Panitia IBF 2011 bekerja sama dengan Yayasan Peduli Matematika Indonesia menyelenggarakan INDONESIA MATHEMATICS COMPETITION 2011 Tingkat SISWA SD, SMP, SMA (Beregu*) dan GURU SD, SMP, SMA (Individu).
*Setiap sekolah dapat mengirimkan maksimal 3 regu @ 3orang. Dalam setiap regu boleh berasal dari satu tingkat kelas atau campuran. Sistem penilaiannya = (Jumlah nilai ketiga peserta dalam setiap regu) dibagi 3 dan dalam pengerjaannya, setiap peserta bekerja secara individu.
TEMPAT DAN WAKTU PELAKSANAAN
INDONESIA MATHEMATICS COMPETITION diselenggarakan di Istora Senayan Jakarta pada tanggal 28, 29, dan 30 November 2011 dengan rincian sebagai berikut.
*Setiap sekolah dapat mengirimkan maksimal 3 regu @ 3orang. Dalam setiap regu boleh berasal dari satu tingkat kelas atau campuran. Sistem penilaiannya = (Jumlah nilai ketiga peserta dalam setiap regu) dibagi 3 dan dalam pengerjaannya, setiap peserta bekerja secara individu.
TEMPAT DAN WAKTU PELAKSANAAN
INDONESIA MATHEMATICS COMPETITION diselenggarakan di Istora Senayan Jakarta pada tanggal 28, 29, dan 30 November 2011 dengan rincian sebagai berikut.
RUANG LINGKUP SOAL
- Bilangan, Aljabar, Geometri dan Pengukuran, dan Statisika dan Peluang (SD & SMP)
- Bilangan, Aljabar, Geometri dan Pengukuran, Statisika dan Peluang, Kalkulus, dan Trigonometri (SMA)
- Soal-soal yang diujikan merupakan soal nonrutin (problem solving) sesuai dengan standar Olimpiade Sains Nasional (OSN)
TIM JURI
Tim yang dibentuk oleh Yayasan Peduli Matematika Indonesia
TEMPAT, WAKTU, DAN BIAYA PENDAFTARAN
Yayasan Peduli Matematika Indonesia
Jl.Kartini Raya (Ruko 2F), Depok 16431
Telp. (021) 7099 1162, 7721 7672 Fax. (021) 7721 7672
CP: Albert (0812 8554 630), Sukarjo (0813 1596 5162)
Waktu:
5 Oktober - 20 November 2011
Biaya:
Rp100.000,- per regu (Siswa) atau Rp 100.000,- per orang (Guru)
TATA CARA PENDAFTARAN
- Isilah dengan lengkap dan jelas formulir (bisa didownload di bagian atas). Formulir bisa digunakan untuk siswa atau guru pendaftar.
- Transfer biaya pendaftaran Ke:
Bank Mandiri KCP Jkt Cimanggis
No.Rek: 157-00-0076449-9
a/n. Yayasan Peduli Matematika Indonesia - Guntinglah bagian bawah formulir sebagai Kartu Peserta untuk dibawa pada saat daftar ulang.
- Kirimkan Formulir dan Bukti Pembayaran melalui:
Fax: (021) 7721 7672
E-mail: mail@peduli-matematika.org (formulir dan bukti pembayaran di-scan terlebih dahulu)
Pos: ke alamat di atas - Lakukan konfirmasi pendaftaran ke nomor telepon di atas.
- Bawa Kartu Peserta (dari potongan formulir) beserta bukti pembayaran (asli) pada saat Daftar Ulang (30 menit sebelum kompetisi).
HADIAH DAN PENGHARGAAN
- Total hadiah uang sebesar Rp50.000.000,- (Medali, Piala, & Uang Tunai)
- Hadiah diberikan kepada tiga regu siswa dan 3 guru dari setiap tingkatan yang memperoleh nilai tertinggi
- Sertifikat juga diberikan kepada guru pendamping/pembimbing
Sumber : Yayasan Peduli Matematika Indonesia
Jumat, 28 Oktober 2011
Work Shop Pembinaan MGMP Matematika
Selama 3 hari dari Selasa, 25 - 27 Oktober telah dilaksanakan Work Shop Pembinaan MGMP Matematika Tingkat DKI Jakarta yang dilaksanakan di SMP Negeri 68 Jakarta. Tujuan dari pelaksanaan Work Shop ini adalah untuk meningkatkan perolehan nilai Ujian Nasional dari tiap-tiap sekolah.
Dalam work shop ini diisi juga dengan bedah SKL oleh Muhammad Ridho, Bedah Silabus dan RPP oleh Bapak Tri Hartono, Penelitian Tindakan (PTK) oleh Bapak Nana, Pembuatan Media Pembelajaran Melalui Power Point (Sulis Riyanto, S.Pd), Soal-soal Matematika Unik (Surachman, S.Pd).
Selama berlangsungnya Work Shop peserta begitu antusias mengikuti setiap sesionnya.
Maju terus MGMP Matematika SMP DKI Jakarta, maju terus pendidikan Indonesia...
Lihat Photo Selengkapnya (Facebook)
.
Dalam work shop ini diisi juga dengan bedah SKL oleh Muhammad Ridho, Bedah Silabus dan RPP oleh Bapak Tri Hartono, Penelitian Tindakan (PTK) oleh Bapak Nana, Pembuatan Media Pembelajaran Melalui Power Point (Sulis Riyanto, S.Pd), Soal-soal Matematika Unik (Surachman, S.Pd).
Selama berlangsungnya Work Shop peserta begitu antusias mengikuti setiap sesionnya.
Maju terus MGMP Matematika SMP DKI Jakarta, maju terus pendidikan Indonesia...
Lihat Photo Selengkapnya (Facebook)
.
മാത്സ് ബ്ലോഗ് പിന്നിട്ടത് 1000 ദിനങ്ങള്‍! സഹസ്രം! സഹര്‍ഷം!!
മാത്സ് ബ്ലോഗ് ആരംഭിച്ചിട്ട് ആയിരം ദിനം പിന്നിട്ടു. ഈ ബ്ലോഗ് ആരംഭിച്ച അന്ന് എത്ര ആവേശത്തോടെയാണ് ഞങ്ങള്‍ ഇതിനായി സമയം മാറ്റി വെച്ചത് അതിലേറെ ആവേശത്തോടെയാണ് ഇന്നും ബ്ലോഗിനു വേണ്ടി സമയം നീക്കി വെക്കുന്നതും. മലയാളികളായ അധ്യാപകരെ കോര്‍ത്തിണക്കാനും അവര്‍ക്കായി ഒരു ചര്‍ച്ചാ വേദി ഒരുക്കാനും സാധിച്ചതില്‍ ഞങ്ങളേറെ സന്തോഷിക്കുന്നു. ബ്ലോഗിനൊപ്പം നിന്നവരുടെ പേരുകള്‍ വിവരിക്കുന്നില്ല. അതിന് ഈ ഒരു വേദി പോരാതെ വരും. ബ്ലോഗിനു വേണ്ടി ആവേശത്തോടെ വാദിക്കുന്ന, ഞങ്ങളെ ഇതേ വരെ നേരിട്ടു കാണാത്തവരായ അനവധി അധ്യാപകരുണ്ട്. അവരാണ് ഞങ്ങളുടെ ബലം.ഈ കൂട്ടായ്മ ഇതിലും ശക്തമായ രീതിയില്‍ തുടര്‍ന്നുകൊണ്ടുപോകുവാന്‍ എല്ലാ സുമനസ്സുകളുടേയും സ്നേഹവും സഹകരണവും കാംക്ഷിക്കുന്നു.
നിങ്ങള്‍ ഞങ്ങളോടൊപ്പം! അതെ ഞങ്ങള്‍ നിങ്ങളോടൊപ്പം!!
ആശംസാ കമന്റുകള്‍ക്കുപരിയായി, ഈ കൂട്ടായ്മ കൂടുതല്‍ വിപുലമാക്കാന്‍ നിങ്ങള്‍ക്കെന്തുചെയ്യാന്‍ കഴിയുമെന്നുകൂടി സൂചിപ്പിക്കാന്‍ സ്നേഹപൂര്‍വ്വം നിര്‍ബന്ധിക്കുന്നു.
Kamis, 27 Oktober 2011
Rene Descartes
In the book 'Problem Solving and Number Theory' I read
Was there no notation for exponents in the time of the great Euler? I did not know how to formulate a query for Google, so I asked a question at Math/StackExchange.
I found out that Descartes introduced the notation for $x^2$. Descartes is famous for his quote "Cogito ergo sum", "Je pense donc je suis" or in plain English "I think, therefore I am". Descartes was my favourite mathematician in secondary school because he invented analytic geometry, one of the milestones in the development of mathematics. Before Descartes geometry was done strictly in the Euclidean way, by compass and ruler. Thanks to Descartes' quadrant and coordinates, geometric shapes like lines and circles could be respresented by algebraic equations. They become objects to do calculations with.
So far about Descartes.
Also, thanks to kind repliers I discovered the bookset "A History of Mathematical Notations, vols 1 and 2., by Florian Cajori". A real gem if you like the history of mathematics. Because the copyright expired one is allowed to freely download the original version. See the comments below the original question at StackExchange for a link to the full version of the book.
Link:
- Question at StackExchange
The law of quadratic reciprocity was discovered for the first time, in a complex form, by L. Euler who published it in his paper entitled “Novae demonstrationes circa divisores numerorum formae $xx + nyy$.
Was there no notation for exponents in the time of the great Euler? I did not know how to formulate a query for Google, so I asked a question at Math/StackExchange.
I found out that Descartes introduced the notation for $x^2$. Descartes is famous for his quote "Cogito ergo sum", "Je pense donc je suis" or in plain English "I think, therefore I am". Descartes was my favourite mathematician in secondary school because he invented analytic geometry, one of the milestones in the development of mathematics. Before Descartes geometry was done strictly in the Euclidean way, by compass and ruler. Thanks to Descartes' quadrant and coordinates, geometric shapes like lines and circles could be respresented by algebraic equations. They become objects to do calculations with.
So far about Descartes.
Also, thanks to kind repliers I discovered the bookset "A History of Mathematical Notations, vols 1 and 2., by Florian Cajori". A real gem if you like the history of mathematics. Because the copyright expired one is allowed to freely download the original version. See the comments below the original question at StackExchange for a link to the full version of the book.
Link:
- Question at StackExchange
Letters from Rapunzel
But why am I writing about it? This isn't Jen Robinson's wonderful reader's blog, after all.
School is a large part of this girl's life, so her letters to the unknown holder of Box #5567 have many observations about the experience of a bright but unothodox student, dealing with serious family issues.
The first homework we hear about is 'think of ten possible ways that Rapunzel might be rescued from her tower' using 'what we have learned about simple and complex machines.' Not a bad assignment, I think. But Rapunzel (not her real name) writes, "Aaargh. I don't want to learn about simple machines! When is the answer to a problem ever simple? When it's STUPID, that's when." She goes on to say how the assignment is better than what's a typical assignment. She then includes her list of 7 very clever ways to rescue Rapunzel. "Note: Like I said, I'm NOT a slacker. The reason I only listed seven ways of rescue is because I don't want Mr. Cornally - that's my math and science teacher- to get too high an expectation of me this early in the year." (OK, I changed the name.) Later, she writes "I only got half credit for my Rapunzel homework. Mrs. Seisnik did not like the "frivolous" way in which I handled the assignment. "MORE SCIENCE. FEWER SILLY JOKES," she wrote in her crisp block letters. "AND WHERE ARE YOUR OTHER THREE ANSWERS?" As if the assignment were serious in the first place!"
That's probably enough for you to figure out whether you want to read it or not. If you're on the edge, I will tell you one of the
Along the way, she deals with her family problem, fighting her classification as gifted (which she refers to as being a deviant, because of the two standard deviation definition the school pschologist tells her), why you would study the most influential people of the last millenium when you could be thinking about who will be the most influential people of the next millenium, why teachers ask for creative work but don't actually want it, all day in school detention, unlikely and irrelevant math problems, writing what teachers want even when you're not interested, trying to accomplish community change, letters to an author and more.
 |
| herzogbr @ Flickr |
I hope you have the chance to find it if you're interested. Regardless, may you help your students learn to make their own progress. As Rapun el writes at one point,
"P.S. It's hard rescuing yourself."
Selasa, 25 Oktober 2011
ശാസ്ത്രമേളയുടെ ഓഫ്ലൈന് സോഫ്റ്റ്‌വെയര്‍ ഇന്‍സ്റ്റലേഷന്‍
ഇക്കൊല്ലത്തെ സ്കൂള്‍ ശാസ്ത്ര-ഗണിതശാസ്ത്ര-സാമൂഹ്യശാസ്ത്ര-ഐടി പ്രവൃത്തിപരിചയ മേളകള്‍ പൂര്‍ണമായും ഓണ്‍ലൈനാക്കാനുള്ള സംവിധാനം ഐടി.@സ്കൂള്‍ ഏര്‍പ്പെടുത്തിയിരിക്കുകയാണല്ലോ. ഇതോടെ വിദ്യാഭ്യാസ വകുപ്പിലെ എല്ലാ മേളകളും ഐടി@സ്കൂളിന്റെ നേതൃത്വത്തില്‍ ഇലക്ട്രോണിക് സംവിധാനത്തിലേക്ക് മാറും. ഒരൊറ്റ ഇന്റര്‍ഫേസില്‍ അഞ്ചുമേളകളും (ശാസ്ത്രം, ഗണിതശാസ്ത്രം, സാമൂഹ്യശാസ്ത്രം, ഐ.ടി. പ്രവൃത്തിപരിചയം) നടത്താന്‍ കഴിയുന്ന വിധത്തിലാണ് പോര്‍ട്ടലിന്റെ ഘടന. ഇപ്പോള്‍ എല്ലാ സ്ക്കൂളുകളും തന്നെ അവരവരുടെ സ്ക്കൂളില്‍ നിന്നും മത്സരിക്കുന്ന വിദ്യാര്‍ത്ഥികളുടെ പേരുവിവരങ്ങളും മത്സരയിനങ്ങളുമെല്ലാം തന്നെ ഓണ്‍ലൈന്‍ പോര്‍ട്ടലിലേക്ക് എന്റര്‍ ചെയ്തു കഴിഞ്ഞല്ലോ. ഇനി ഇതെല്ലാം കണ്‍ഫേം ചെയ്ത ശേഷം എ.ഇ.ഒ തലത്തില്‍ ഉപജില്ലാതല മത്സരങ്ങളുടെ നടത്തിപ്പിനായി ഇത് csv ഫയല്‍ രൂപത്തില്‍ ഡൗണ്‍ലോഡ് ചെയ്തെടുക്കാന്‍ കഴിയും. ആ വിവരങ്ങള്‍ നമുക്ക് നല്‍കിയിരിക്കുന്ന ഓഫ്ലൈന് സോഫ്റ്റ്‌വെയറിലേക്ക് ഇംപോര്‍ട്ട് ചെയ്യുകയും തുടര്‍ന്ന് പാര്‍ട്ടിസിപ്പന്റ് കാര്‍ഡ്, ടാബുലേഷന്‍, സര്‍ട്ടിഫിക്കറ്റ് എന്നിവ പ്രിന്റെടുക്കാനും കഴിയും. ഇപ്രകാരം ടാബുലേഷനും മറ്റും ചെയ്തെങ്കില്‍ മാത്രമേ ഉപജില്ലാതല മത്സരവിജയികളുടെ വിവരങ്ങളടങ്ങിയ csv ഫയല്‍ ജില്ലാ തല മേളയ്ക്കായി ജില്ലാകണ്‍വീനര്‍മാര്‍ക്ക് നല്‍കാന്‍ കഴിയൂ. അതുകൊണ്ടു തന്നെ സബ്ജില്ലാതല മത്സരങ്ങളുടെ എല്ലാ ഘട്ടവും ഈ ഓഫ്ലൈന് സോഫ്റ്റ്‌വെയറിലേക്ക് എന്റര്‍ ചെയ്യേണ്ടത് അതാത് സബ്‌ജില്ലാ കണ്‍വീനര്‍മാരുടെ ചുമതലയാണ്. എങ്ങിനെയാണ് നമുക്ക് ലഭിച്ച ഓഫ്ലൈന് സോഫ്റ്റ്‌വെയറിന്റെ ഇന്‍സ്റ്റലേഷന്‍ നടത്തുക? അതിനുള്ള സ്റ്റെപ്പുകള്‍ ചുവടെ നല്‍കിയിരിക്കുന്നു.1. നമ്മുടെ കയ്യിലുള്ള ശാസ്ത്രമേളയുടെ tar.gz എന്ന എക്സ്റ്റെന്‍ഷനുള്ള ഫയല്‍ എക്സ്ട്രാക്ട് ചെയ്യുക. (ഫയലില്‍ റൈറ്റ് ക്ലിക്ക് ചെയ്ത് extract here എന്നു നല്‍കിയാലും മതി)
2. മുകളില്‍ കാണുന്നതു പോലെ software എന്ന ഫോള്‍ഡറും, installer, lampstart, lampstop, scf_sub_users.pdf, എന്നീ നാലു ഫയലുകളും എക്സ്ട്രാക്ട് ചെയ്യുമ്പോള്‍ കാണാന്‍ കഴിയും.
3. ഇതില്‍ Installer എന്ന ഫയലില്‍ റൈറ്റ് ക്ലിക്ക് ചെയ്ത് Properties എടുത്ത ശേഷം അതിലെ permissions മെനുവെടുത്ത് execute പെര്‍മിഷനില്‍ ടിക് നല്‍കുക.
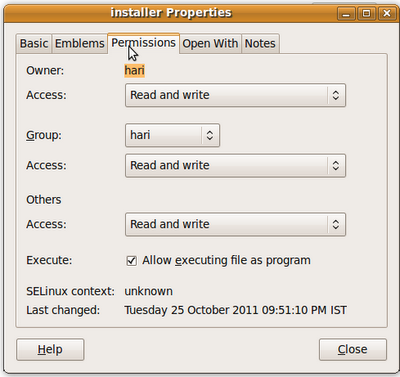
4. തുടര്‍ന്ന് Installer ഫയലില്‍ ഡബിള്‍ക്ലിക്ക് ചെയ്യുമ്പോള്‍ വരുന്ന ജാലകത്തില്‍ Run in terminal ല്‍ ക്ലിക്ക് ചെയ്യുക.
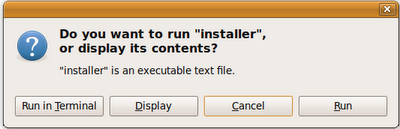5. ഈ സമയം ടെര്‍മിനല്‍ തുറക്കപ്പെടുകയും താഴെ കാണുന്ന പോലെ റൂട്ട് പാസ്വേഡ് ചോദിച്ചു കൊണ്ടുള്ള ജാലകം പ്രത്യക്ഷപ്പെടുകയും ചെയ്യും.Installing Subdistrict Science Fair Software... .
Please enter root's password.
[sudo] password for XXXX:
റൂട്ട് പാസ്വേഡ് നല്‍കിക്കഴിയുമ്പോള്‍ ഇന്‍സ്റ്റലേഷന്‍ നടക്കുന്നത് നമുക്കു കാണാം.
Installation completed. Close This Terminal or press Ctrl+C എന്ന മെസ്സേജ് വരുന്നതോടെ ഇന്‍സ്റ്റലേഷന്‍ പൂര്‍ത്തിയായതായി കണക്കാക്കാം. മെസ്സേജില്‍ പറഞ്ഞ പോലെ ടെര്‍മിനല്‍ ക്ലോസ് ചെയ്യാനായി കണ്‍ട്രോള്‍ കീയും c ബട്ടണും കൂടി ഒരുമിച്ച് പ്രസ് ചെയ്യുക.
NB: ഇന്‍സ്റ്റലേഷന്‍ കഴിഞ്ഞാല്‍ installer എന്ന ഫയല്‍ ഡിലീറ്റ് ചെയ്തു കളയുക. കാരണം, ഡാറ്റാ എന്‍ട്രിക്കിടെ അറിയാതെയെങ്ങാന്‍ installer ഫയലില്‍ ക്ലിക്ക് ചെയ്തു പോയാല്‍ വീണ്ടും ഇന്‍സ്റ്റലേഷന്‍ നടക്കുകയും എന്റര്‍ ചെയ്ത എല്ലാ വിവരങ്ങളും നഷ്ടപ്പെടുകയും ചെയ്യും.
6. ഇനി നമുക്ക് ഓഫ്ലൈന് സോഫ്റ്റ്‌വെയര്‍ തുറക്കാം. അതിനായി മോസില്ല ഫയര്‍ഫോക്സ് ബ്രൗസര്‍ എടുത്ത് അതില്‍ localhost എന്നു ടൈപ്പ് ചെയ്ത് എന്റര്‍ ചെയ്യുക. ഉടന്‍ താഴെ കാണിച്ചിരിക്കുന്ന ശാസ്ത്രമേളയുടെ ഓഫ്ലൈന് സോഫ്റ്റ്‌വെയറിന്റെ ഹോംപേജ് തുറന്നു വരുന്നു.
7 ഇവിടെ യൂസര്‍ നെയിമും പാസ്വേഡും നല്‍കുക. ഇതു രണ്ടും ആദ്യം എക്സ്ട്രാക്ട് ചെയ്തു വെച്ചിരിക്കുന്ന ഫോള്‍ഡറിലെ scf_sub_users.pdf എന്ന ഫയലില്‍ നിന്നു കണ്ടെത്താം. അതില്‍ നമ്മുടെ സബ്ജില്ലയുടെ പേരില്‍ രണ്ടു യൂസര്‍ നെയിമും പാസ്വേഡും കാണാന്‍ കഴിയും. അതില്‍ രണ്ടാമത്തേതായി സബ്ജില്ലയുടെ പേരിനൊപ്പം codeuser എന്നു കാണുന്ന യൂസര്‍നെയിം നമുക്ക് വര്‍ക്ക് എക്സ്പീരിയന്‍സിന് മത്സരങ്ങളുടെ കോഡ് ജനറേറ്റ് ചെയ്യാന്‍ വേണ്ടി മാത്രമുള്ളതാണ്. അതുകൊണ്ടു തന്നെ മറ്റുപയോഗങ്ങള്‍ക്ക് നമ്മുടെ സബ്ജില്ലയുടെ പേരുള്ള ആദ്യത്തെ യൂസര്‍നെയിമും (codeuser എന്ന് ഒപ്പമില്ലാത്തത്) അതിന്റെ പാസ്വേഡും തന്നെ ഉപയോഗിക്കുക.
NB: നമ്മുടേതല്ലാത്ത മറ്റേതെങ്കിലും ഉപജില്ലയുടെ യൂസര്‍ നെയിമും പാസ്വേഡും നല്‍കിയാണ് ലോഗിന്‍ ചെയ്തിരിക്കുന്നതെങ്കില്‍ 9-ം സ്റ്റെപ്പില്‍ പറഞ്ഞിരിക്കുന്ന പോലെ പോര്‍ട്ടലില്‍ നിന്നും ഡൗണ്‍ലോഡ് ചെയ്തെടുത്ത വിവരങ്ങള്‍ നമുക്ക് ഇംപോര്‍ട്ട് ചെയ്യാന്‍ സാധിക്കില്ല. പേജിനുമുകളില്‍ ചുവന്ന ബോക്സില്‍ invalid CSV എന്ന മെസ്സേജ് വന്നിരിക്കും. പോര്‍ട്ടലില്‍ നിന്ന് വിവരങ്ങള്‍ എക്സ്പോര്‍ട്ട് ചെയ്തപ്പോള്‍ സംഭവിച്ച പിശകുകള്‍ മൂലവും ഇതേ മെസ്സേജ് വന്നേക്കാം.
8. ഇനി വരിക പാസ്വേഡ് മാറ്റാനുള്ള പേജായിരിക്കും. പഴയ പാസ്വേഡ് നല്‍കിയ ശേഷം പുതിയ പാസ്വേഡ് രണ്ടു വട്ടം നല്‍കി ആദ്യലോഗിന്‍ ചെയ്യുന്നയാളിന്റെ പേര്, ഫോണ്‍, ഇമെയില്‍ എന്നിവ നല്‍കാനായിരിക്കും നിര്‍ദ്ദേശം.
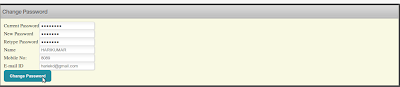തുടര്‍ന്ന് Change password ല്‍ ക്ലിക്ക് ചെയ്യാം.9. ഈ സമയം വരിക പോര്‍ട്ടലില്‍ നിന്നും ഡൗണ്‍ലോഡ് ചെയ്തെടുത്ത csv ഫയലുകള്‍ ഇംപോര്‍ട്ട് ചെയ്യാനുള്ള പേജായിരിക്കും. തങ്ങളുടെ ഉപജില്ലയിലുള്ള എല്ലാ സ്ക്കൂളുകളും വിവരങ്ങള്‍ കൃത്യമായി നല്‍കി Confirm ചെയ്തുവെന്ന് ഉറപ്പു വരുത്തിയ ശേഷം എ.ഇ.ഒ അഡ്മിന് CSV ഫയലുകള്‍ പോര്‍ട്ടലില്‍ നിന്ന് എക്സ്പോര്‍ട്ട് ചെയ്തെടുക്കാം. അത് ഓരോന്നോരോന്നായി ഇംപോര്‍ട്ട് ചെയ്യാം. ഓരോന്നും ഇംപോര്‍ട്ട് ചെയ്യുന്നതിനനുസരിച്ച് താഴെ Statusല്‍ imported എന്ന മെസ്സേജ് കാണിച്ചു കൊണ്ടിരിക്കും. പച്ച നിറത്തില്‍ csv data Saved successfully എന്ന മെസ്സേജും മുകളില്‍ കാണാം. പിശകുണ്ടെങ്കില്‍ Failed to Save CSV Data എന്നായിരിക്കും വരിക. ആദ്യത്തെ csv ഫയല്‍ ഇംപോര്‍ട്ട് ചെയ്യുമ്പോള്‍ തന്നെ പേജിനു മുകള്‍ ഭാഗത്തായി മെനുവിന്റെ പാനല്‍ പ്രത്യപ്പെട്ടിട്ടുണ്ടാകും. ഓരോ മെനുവിനെക്കുറിച്ചും താഴെയുള്ള Help fileല്‍ വിശദമാക്കിയിട്ടുണ്ട്.
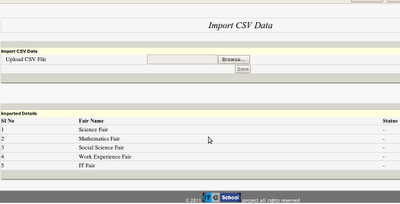
10. പക്ഷെ ഒരു കാര്യം പ്രത്യേകം ഓര്‍മ്മിക്കുക. ഒരു ഉപജില്ലയിലെ ഏത് മേളയ്ക്ക് വേണ്ടിയാണോ ഈ സിസ്റ്റം ഉപയോഗിക്കുന്നത്, ആ മേളയുമായി ബന്ധപ്പെട്ട കാര്യങ്ങള്‍ ആ സിസ്റ്റത്തില്‍ മാത്രമേ നല്‍കാവൂ. മാത്രമല്ല, സിസ്റ്റം ഓഫ് ചെയ്യുന്നതിന് മുന്‍പ് lampstop എന്ന ഫയല്‍ റണ്‍ ചെയ്ത് വെബ്സെര്‍വര്‍ ക്ലോസ് ചെയ്യണം. ഇല്ലെങ്കില്‍ എന്തെങ്കിലും തരത്തിലുള്ള ക്രാഷ് സംഭവിച്ചാല്‍ ഡാറ്റ മുഴുവന്‍ നഷ്ടപ്പെട്ടേക്കാം. അതുപോലെ തന്നെ ഷട്ട്ഡൗണ്‍ ചെയ്ത കമ്പ്യൂട്ടര്‍ തുറന്ന് സോഫ്റ്റ്‌വെയര്‍ പ്രവര്‍ത്തിപ്പിക്കുന്നതിന് മുന്‍പ് എക്സ്ടാക്ട് ചെയ്ത ഫോള്‍ഡറിലെ lampstart എന്ന ഫയല്‍ റണ്‍ ചെയ്യണം. എന്നാലേ പ്രോഗ്രാം പ്രവര്‍ത്തനസജ്ജമാകൂ.
ഇനിയുള്ള വിവരങ്ങളെല്ലാം ചിത്രസഹിതം വിശദമായി താഴെയുള്ള പി.ഡി.എഫ് ഫയലില്‍ നല്‍കിയിട്ടുണ്ട്.
Click here for Sastramela offline Software Help file
ഇതു നോക്കി മനസ്സിലാക്കുമല്ലോ. നിങ്ങളുടെ അഭിപ്രായങ്ങള്‍ പങ്കുവെക്കണേ.
Senin, 24 Oktober 2011
Ten Rules for Game Design
 |
| All rights (c) Hasbro. |
1) Goal(s).Usually easy for educational games.
But wait... maybe not. Teachers are used to setting objectives, but the kind of objective makes a big difference in the game. If in addition to content objectives, the teacher has process objectives, it can make a big difference in the game. The good news for mathies is that any game with strategy feels like it's connecting to the problem solving process.
2) Rules.Rules need to be understandable, but make things hard enough for the player. I think some ed games have trouble here, because of the old saw about about good teachers make things easy for their students. Goes well, however, with the resurgence of the 'be less helpful' mode of teaching. (We can't call it new if Dewey was onto it.)
3) Interaction.
4) Catch-Up.If a player who falls behind has no chance, it disengages them. I just recently noticed how much this matters to me. I think because as a game lover, this is one of the few things I loathe about them. Think about the slow grinding Monopoly death... (shudder) Within the game, players need to be able to catch up. It doesn't have to be likely - then it's Candy Land, where you can't keep a lead. You might as well be teleporting around that board. It does have to be possible, which will help create stories of the epic win.
In educational games this is a double danger, since so many ed games reward players who've already learned the material. If a math game is about who's fastest, there are students who start the game knowing there's no hope. Sometimes this is an easy fix by adding a bit of chance, but usually it requires structural design. I think this principle is why so many games get pushed to review in the classroom, instead of being used to help learn.
5) Inertia.Leave them wanting more. Get out while the getting's good. Dave Coffey is excellent at this with his lessons, always leaving students something to think about on the way home. I measure this by whether students are 'whew' or 'ohhhhh' when our time is up. In my experience this connects heavily with (2), Rules. Too easy or too hard shows up here.
Mark connects it with writing advice: make it as short as you can, then cut 10%.
Also tough for teachers, because we're trained to go until everyone finishes. Much better to have people sitting around doing nothing (quietly, of course) than to have anyone not have a chance to finish. That's murder to a game.
So Far So Good
I'd be really interested in hearing other people's ideas about this. Not sure where the best venue is ... maybe the Linked In game based learning group?
If his list next week is as good as this week's look for my part 2 next Monday! I'm enjoying wondering what the next five things must be...
It was 2 weeks! My 2nd part is up, with links to Mark's 2nd part.
Image credits: Usonian, Kathy Cassidy @ Flickr
Minggu, 23 Oktober 2011
Social Media for mathematicians
The places 'to be' for mathematicians are -not- Twitter and facebook, although they are both great places to socialize, chit-chat you know what I mean, they basically steal your valuable time.
Mathematicians hang out at:
- http://math.stackexchange.com/
- http://www.reddit.com/r/math
- http://www.stumbleupon.com/to/stumble/topic:247
- http://mathoverflow.net/
- http://mathblogging.org/
- http://arxiv.org/
Thanks to Gaurav Tiwari, read his review at his own site My Digital Notebook
Mathematicians hang out at:
- http://math.stackexchange.com/
- http://www.reddit.com/r/math
- http://www.stumbleupon.com/to/stumble/topic:247
- http://mathoverflow.net/
- http://mathblogging.org/
- http://arxiv.org/
Thanks to Gaurav Tiwari, read his review at his own site My Digital Notebook
Sabtu, 22 Oktober 2011
The difference between mathematics and numerology
Numerologist is a four-letter word among mathematicians ( I can imagine ). Is numerology the same as number theory? Not really, the difference between numerology and number theory, as a branch of mathematics, can best be explained using an example.
Both numerologists and mathematicians study identities like $$2^2 + 3^2 + 5^2 + 7^2 + 11^2 + 13^2 + 17^2 = 666.$$ A mathematician would notice that this is the sum of the first seven primes and rewrite the sum as $$\sum_{k=1}^{7} p_k = 666.$$ The right-hand side sum is a number with equal digits, so the mathematician might look at other sums of consecutive primes and verify if these sums have similar patterns. Basically a mathematician is interested in anything that might lead to the formulation of a theorem, a proposition to prove mathematically.
A numerologist would immediately notice that $666$ is the number of "The Beast", the representation of evil in the Christian belief system. Then, a numerologist might consider prime numbers divine, since they are the building blocks of all integers, and might try to formulate some law of good and bad represented in the sum-formula. Numerologists also believe that future events can be predicted so they will be extra alert to that.
I believe that it was until the Middle Ages that there was no real distinction between the profession of numerologist and mathematician. Newton has been called the last Alchemist, perhaps he was the last mathematician / numerologist as well. ( History, I am afraid, is not my strongest point. )
Both numerologists and mathematicians study identities like $$2^2 + 3^2 + 5^2 + 7^2 + 11^2 + 13^2 + 17^2 = 666.$$ A mathematician would notice that this is the sum of the first seven primes and rewrite the sum as $$\sum_{k=1}^{7} p_k = 666.$$ The right-hand side sum is a number with equal digits, so the mathematician might look at other sums of consecutive primes and verify if these sums have similar patterns. Basically a mathematician is interested in anything that might lead to the formulation of a theorem, a proposition to prove mathematically.
A numerologist would immediately notice that $666$ is the number of "The Beast", the representation of evil in the Christian belief system. Then, a numerologist might consider prime numbers divine, since they are the building blocks of all integers, and might try to formulate some law of good and bad represented in the sum-formula. Numerologists also believe that future events can be predicted so they will be extra alert to that.
I believe that it was until the Middle Ages that there was no real distinction between the profession of numerologist and mathematician. Newton has been called the last Alchemist, perhaps he was the last mathematician / numerologist as well. ( History, I am afraid, is not my strongest point. )
Solving quadratic congruence equations in Mathematica
This is as yet the last post in the LQR series. If you are only interested in -solving- ( quadratic ) congruence equations then this is the way to do it in Mathematica:
As a general Diophantic equation:
Or slightly more elegant as a pure congruence equation ( thanks to: Mr. Wizard ):
As a general Diophantic equation:
In[1]:= Reduce[x^2==123456+1299709 k,{x,k},Integers]
Out[1]= (C[1]\[Element]Integers&&x==427784-1299709 C[1]&&k==140800-855568 C[1]+1299709 C[1]^2)||(C[1]\[Element]Integers&&x==871925-1299709 C[1]&&k==584941-1743850 C[1]+1299709 C[1]^2)Or slightly more elegant as a pure congruence equation ( thanks to: Mr. Wizard ):
In[2]:= Reduce[x^2 == 123456, x, Modulus -> 1299709]
Out[2]= x == 427784 || x == 871925
Jumat, 21 Oktober 2011
Shanks-Tonelli algorithm for solving quadratic modular equations
M381 unit 6 is about the Law of Quadratic Reciprocity. An application of the LQR is solving quadratic modular equations like: $$x^2 \equiv 499 \ \text{mod(617)}.$$ M381 contains a method that can fast determine if that equation is solvable. It does not contain however a fast algorithm for finding the actual solutions. One such algorithm is the Shanks-Tonelli algorithm and can be found on Planet Math which as often gives a much clearer presentation than the messy Wikipedia-entry.
See also: Tutorial for Quadratic Equations
See also: Tutorial for Quadratic Equations
Quadratic reciprocity in a finite group.
Law of Quadratic Reciprocity
Let $p$ and $q$ be distinct odd primes. Then $$\displaystyle \left({\frac p q}\right) \left({\frac q p}\right) = \left({-1}\right)^{\frac {\left({p-1}\right) \left({q-1}\right)} 4}$$ where $\displaystyle \left({\frac p q}\right)$ and $\displaystyle \left({\frac q p}\right)$ are defined as the Legendre Symbol $\displaystyle \left({\frac{a}{p}}\right) := a^{\frac{(p-1)}{2}} \pmod p$.Gauss considered his work on the Quadratic Reciprocity Law among his major achievements. I don't 'get that', not now anyway, that's a call for more study on the topic.
Now and then, when I browse through papers, or otherwise, I find an interesting mathematical paper... ( that I can actually read ). Actually, I was browsing through a book called Reciprocity Laws, from Euler to Eisenstein by Franz Lemmermeyer, it contains more than 100 proofs of the Quadratic Reciprocity Law. I hoped to find a proof I could appreciate by it's beauty. Although most proofs are based on Gauss's Lemma ( as the proof in M381 ) but there are proofs in other realms of mathematics like Group Theory. Group Theory -as we know it today- did not exist in Gauss's time. That's why I am going to spend some time studying the following paper 'Quadratic reciprocity in a finite group.'
Kamis, 20 Oktober 2011
2nd Fundamental Theorem of Calculus
Our last calculus class looked into the 2nd Fundamental Theorem of Calculus (FTOC). We talked through the first FTOC last week, focusing on position velocity and acceleration to make sense of the result. Our interpretation was that the FTOC-1 finds the area by using the anti-derivative. How are those connected?
This week we wanted to peek at the 2nd part. (OK, it was me.) We looked up the result on Mathworld, and talked about barriers to understanding. The teachers identified that the conflation between the antiderivative and the integral (meaning area under a curve) is almost total, so that the theorem is just restating what we already think. Using this completely confusing notation and totally new way to define a function. Perfect situation for a GeoGebra sketch to allow students to explore.
This sketch uses several GGB4 features. It uses the integral[ ] command to find the area under a curve, which I would have had to cheat before, the input boxes to allow real freedom of entering a function, and buttons so that students don't have to know GeoGebra commands to refresh the view. This is my first sketch uploaded to GeoGebraTube, which is a huge improvement over the old webhosting at geogebra.org. You can link to a teacher page or a student page, there's a link to download the file, and there's easy to find embed code. Best of all, the front page has a search, and shows recent uploads so it's fun just to check in. And everything uploaded is CC3.0; darn near ideal resource.
If the embed code worked on blogger, I would have put it right here. (That's why only darn near ideal.)
The teachers noticed all sorts of interesting things, recognizing anti-derivatives, seeing the +C (constant of integration) in action, and seemed to make sense of the integral definition of a function. They picked interesting functions to try, like increasing degrees of polynomials, trigonometric functions, functions without an analytic antiderivative (like cos(x^2)) and the fabulous e^x.
I've added the grid in to help students see the area more clearly, and set the grid to distance 1 to keep it unit sized. Linda Fahlberg and John Scammell helped me with the right script for the button with quick Twitter responses. ZoomIn[1] to get a CTRL-F (refresh view) effect, and UpdateConstruction[] to get a CTRL-R effect (recompute all objects). (Written down so I will never forget again.)
Photo credit: ajlvi @ Flickr. He (?) said he tried to capture everything he needed to know for the GRE on the board and then take a picture, but it was illegible on his phone. If he's that clever, I'm sure he did fine.
This week we wanted to peek at the 2nd part. (OK, it was me.) We looked up the result on Mathworld, and talked about barriers to understanding. The teachers identified that the conflation between the antiderivative and the integral (meaning area under a curve) is almost total, so that the theorem is just restating what we already think. Using this completely confusing notation and totally new way to define a function. Perfect situation for a GeoGebra sketch to allow students to explore.
This sketch uses several GGB4 features. It uses the integral[ ] command to find the area under a curve, which I would have had to cheat before, the input boxes to allow real freedom of entering a function, and buttons so that students don't have to know GeoGebra commands to refresh the view. This is my first sketch uploaded to GeoGebraTube, which is a huge improvement over the old webhosting at geogebra.org. You can link to a teacher page or a student page, there's a link to download the file, and there's easy to find embed code. Best of all, the front page has a search, and shows recent uploads so it's fun just to check in. And everything uploaded is CC3.0; darn near ideal resource.
If the embed code worked on blogger, I would have put it right here. (That's why only darn near ideal.)
 |
| Click here to go to the sketch on GeoGebraTube. |
The teachers noticed all sorts of interesting things, recognizing anti-derivatives, seeing the +C (constant of integration) in action, and seemed to make sense of the integral definition of a function. They picked interesting functions to try, like increasing degrees of polynomials, trigonometric functions, functions without an analytic antiderivative (like cos(x^2)) and the fabulous e^x.
I've added the grid in to help students see the area more clearly, and set the grid to distance 1 to keep it unit sized. Linda Fahlberg and John Scammell helped me with the right script for the button with quick Twitter responses. ZoomIn[1] to get a CTRL-F (refresh view) effect, and UpdateConstruction[] to get a CTRL-R effect (recompute all objects). (Written down so I will never forget again.)
Photo credit: ajlvi @ Flickr. He (?) said he tried to capture everything he needed to know for the GRE on the board and then take a picture, but it was illegible on his phone. If he's that clever, I'm sure he did fine.
Selasa, 18 Oktober 2011
Elegi Bagaimana Matematikawan Dapat Mengusir Syaitan?
Oleh Marsigit
Syaitan:
Uhiiihhhhh....suaraku melengking...
Matematikawan:
Melengking ditambah melengking sama dengan dua melengking.
Melengking dikurangi melengking sama dengan nol melengking.
Melengking kali melengking sama dengan melengking kuadrat.
Melengking pangkat melengking sama dengan melengking kali melengking dst sampai melengking kali.
Melengking dibagi melengking sama dengan satu
Syaitan:
Uhiiihhhhh....suaraku melengking...
Matematikawan:
Melengking ditambah melengking sama dengan dua melengking.
Melengking dikurangi melengking sama dengan nol melengking.
Melengking kali melengking sama dengan melengking kuadrat.
Melengking pangkat melengking sama dengan melengking kali melengking dst sampai melengking kali.
Melengking dibagi melengking sama dengan satu
An easy problem
A wise man rode into a desert village one evening as the sun was setting. Dismounting from his camel, he asked one of the villagers for a drink of water.‘Of course,’ said the villager and gave him a cup of water. The traveller drank the whole cupful. ‘Thank you,’ he said. ‘Can I help you at all before I travel on?’‘Yes,’ said the young man. ‘We have a dispute in our family. I am the youngest of three brothers. Our father died recently, God rest his soul, and all he possessed was a small herd of camels. Seventeen, to be exact. He decreed in his will that one half of the herd was to go to my oldest brother, one third to the middle brother and one ninth to me. But how can we divide a herd of 17? We do not want to chop up any camels, they are worth far more alive.’ ‘Take me to your house,’ said the sage. When he entered the house he saw the other two brothers and the man’s widow sitting around the fire arguing. The youngest brother interrupted them and introduced the traveller.
‘Wait,’ said the wise man, ‘I think I can help you. Here, I give you my camel as a gift. Now you have 18 camels. One half goes to the eldest, that’s nine camels. One third goes to the middle son, that’s six camels. And one ninth goes to my friend here, the youngest son. That’s two.’ ‘That’s only 17 altogether,’ said the youngest son. ‘Yes. By a happy coincidence, the camel left over is the one I gave to you. If you could possibly give it back to me, I will continue on my journey.’ And he did.
What went wrong ?
A difficult problem
Prove or disprove the existence of God.
Answering this question requires a definition of God, which we don't have of course. We could propose a temporarily definition like 'God is the entity that created life on planet Earth, a modest definition because it leaves the question of who created the universe unanswered.
Although still debated, Gödel's incompleteness theorems imply that we won't be able to build computers with a conscious mind capable of creating new mathematics or writing a program that solves all open problems in mathematics. Besides cloning and modifying what we have ( DNA ) we won't be able to create a 'machine' smarter than ourselves.
Our own existence is a paradox we don't understand. History proves that in cases like that humans are creative in inventing a God capable of fixing any problem. Despite centuries of scientific advances we still need a God to explain our existence.
Sabtu, 15 Oktober 2011
അര്‍ജുനന്റെ ഉത്തരങ്ങളും ഒരമ്മയുടെ കത്തും
നേരത്തേ കോട്ടയത്തുനിന്നും അര്‍ജുന്‍ ഫിസിക്സ് ചോദ്യോത്തരങ്ങള്‍ പ്രസിദ്ധീകരിച്ചത് ഓര്‍മ്മ കാണുമല്ലോ. ഇന്നത്തെ നിലയില്‍ ബഹുഭൂരിപക്ഷം കുട്ടികളും ചെയ്യാനൊരുമ്പെടാത്ത ഒരു പ്രവര്‍ത്തനത്തിനാണ് അര്‍ജുന്‍ മുന്‍കൈയ്യെടുത്തത്. ആ കുട്ടി തയ്യാറാക്കിയ ഫിസിക്സ് ചോദ്യോത്തരങ്ങളില്‍ അപൂര്‍വം ചില ഉത്തരങ്ങളില്‍ ചില തിരുത്തുകളും വിശദീകരണങ്ങളും വേണ്ടി വന്നിരുന്നു. നമ്മുടെ ഫിസിക്സ് അധ്യാപകര്‍ അഭിനന്ദനാര്‍ഹമായ വിധം അതില്‍ ഇടപെട്ട് ചോദ്യോത്തരങ്ങള്‍ കുറ്റമറ്റതാക്കാന്‍ സഹായിക്കുകയും ചെയ്തു. ഒരു വിദ്യാര്‍ത്ഥി എന്ന നിലയില്‍ ആ കുട്ടി താനെഴുതിയ ഉത്തരങ്ങള്‍ ആധുനിക സാങ്കേതിക വിദ്യയായ ഇന്റര്‍നെറ്റിലൂടെ ഒരു ചര്‍ച്ചയ്ക്ക് വിധേയമാക്കുകയും വിശദീകരണങ്ങളര്‍ഹിക്കുന്നവ മനസിലാക്കിയെടുക്കുകയും ചെയ്തു. അതില്‍ നിന്നെല്ലാം പ്രചോദനമുള്‍ക്കൊണ്ട് അര്‍ജുന്‍ തികഞ്ഞ സമര്‍പ്പണത്തോടെ ചോദ്യബാങ്കിലുണ്ടായിരുന്ന സമാന്തരശ്രേണിയിലെ ചില ചോദ്യങ്ങളുടെ ഉത്തരമെഴുതുന്നു. ഈ പോസ്റ്റിനൊപ്പം അതു കൂടി മാത്സ് ബ്ലോഗ് പ്രസിദ്ധീകരിക്കുകയാണ്.
അര്‍ജ്ജുനന്‍മാരെ വളര്‍ത്തിയെടുക്കണം. അധ്വാനിക്കാന്‍ സന്നദ്ധരാകുന്ന ഒരു തലമുറയെ നമുക്കാവശ്യമുണ്ട്. അവര്‍ക്ക് തെറ്റു പറ്റിക്കോട്ടേ. തിരുത്താന്‍ അധ്യാപകരായ നമ്മള്‍ ഒപ്പമില്ലേ? തന്റെ വിദ്യാലയത്തിലെ കുട്ടി എഴുതുന്ന ഒരു ലേഖനത്തിലോ അല്ലെങ്കില്‍ ചോദ്യോത്തരങ്ങളിലോ തെറ്റു വന്നാലോ എന്ന ദുരഭിമാനം അധ്യാപകര്‍ക്കാവശ്യമുണ്ടോ? ഇതല്ലേ, യഥാര്‍ത്ഥ വിദ്യാഭ്യാസം? ഇത്തരത്തിലുള്ള ഒരു കുട്ടി തങ്ങളുടെ വിദ്യാലയത്തില്‍ ഉണ്ടായിരുന്നെങ്കില്‍ എന്ന് ഏത് അധ്യാപകരാണ് ആഗ്രഹിച്ചു പോകാത്തത്? ഇക്കൂട്ടരും നമുക്കു മുന്നിലുണ്ട്. കണ്ടെത്താന്‍ നമ്മുടെ കണ്ണുകള്‍ തുറക്കുന്നില്ല എന്നതാണ് നമ്മുടെ പോരായ്മ. പിന്നെ നമ്മുടെ ടീം അംഗം മുരളിസാര്‍ അയച്ചുതന്ന സമാന്തരശ്രേണിയിലെ ഉത്തരങ്ങളുടെ പുതിയ സമീപനം.
ഇടയ്ക്ക് മറ്റൊരു കാര്യം സൂചിപ്പിക്കട്ടെ. കഴിഞ്ഞ ദിവസം ജോണ്‍ സാറിന് ഒരു പോസ്റ്റ്കാര്‍ഡ് തപാലില്‍ എത്തി. കത്തിലെ വരികള്‍ മാത്സ് ബ്ലോഗിന് നാളിതു വരെ ലഭിച്ചിട്ടുള്ള അനുമോദനങ്ങള്‍ക്കും പ്രോത്സാഹനങ്ങളെക്കാളുമെല്ലാം വിലമതിക്കുന്ന ഒന്നാണ്. മാത്സ് ബ്ലോഗിന് കത്തെഴുതിയത് ഒരു അധ്യാപികയല്ല. മറിച്ച് ഒരു വീട്ടമ്മയാണെന്നതാണ് ഈ കത്ത് മൂല്യമേറിയതായി ഞങ്ങള്‍ക്ക് മാറാനിടയായത്. അതിലെ വാചകങ്ങള്‍ വള്ളിപുള്ളി വിടാതെ ചുവടെ കുറിക്കട്ടെ.
സര്‍ ,
വിദ്യാര്‍ഥികളും അദ്ധ്യാപകരും മാത്രമല്ല എന്നെപോലുള്ള വീട്ടമ്മമാരും മാത്സ് ബ്ലോഗ് നോക്കാറുണ്ട് .ഇതുവരെ പത്താംക്ലാസിലെ കണക്ക് ചോദ്യശേഖരത്തിന്റെ ഉത്തരം പ്രസിദ്ധീകരിച്ചിട്ടില്ല. എല്ലാ ചോദ്യങ്ങളും ക്ലാസില്‍ ചെയ്യാന്‍ പറ്റില്ലെന്ന് ടീച്ചര്‍ പറയുന്നു. ചിലതൊന്നും കിട്ടുന്നുമില്ല. കുട്ടിയ്ക്ക് ട്യൂഷന്‍ ഇല്ല. എന്താണ് ചെയ്യാന്‍ പറ്റുന്നത്? ഡിസംബറില്‍ വീണ്ടും ചോദ്യങ്ങള്‍ വരുമല്ലോ? ഇതിന്റെ ഉത്തരം സാറും മറ്റുള്ളവരും ചേര്‍ന്ന് തയ്യാറാക്കി പ്രസിദ്ധീകരിക്കുമോ?
എന്ന്
ബിന്ദു സുരേഷ്
ഇങ്ങനെ ഒരു അഭിപ്രായം പറഞ്ഞതിന് ബിന്ദുവിനെ അഭിനന്ദിക്കുന്നു. കാരണമെന്തന്നല്ലേ? മാത്സ് ബ്ലോഗ് എന്നും കുട്ടികളുടെയും അധ്യാപകരുടെയും പക്ഷത്തുനിന്നാണ് ചിന്തിക്കുന്നത് . ചോദ്യങ്ങളുടെ ഉത്തരം കുട്ടി സ്വയം കണ്ടെത്താന്‍ ശ്രമിക്കുകയും പറ്റാതെ വരുമ്പോള്‍ അധ്യാപകരെയോ കണക്കുപഠിച്ചിച്ചുള്ള മറ്റുള്ളവരെയോ സമീപിക്കുകയും ചെയ്യുമെന്ന് പ്രതീക്ഷിക്കുന്നു. പിന്നെ, കുട്ടിക്ക് ഉത്തരം കിട്ടാതെ വരുമ്പോള്‍ ചോദിച്ചാല്‍ പറഞ്ഞുകൊടുക്കാത്ത അധ്യാപകര്‍ ഇന്നത്തെ കാലത്തുണ്ടാകില്ല. തീര്‍ച്ച. കുട്ടിയുടെ പഠനത്തില്‍ അധ്യാപികയും മാതാപിതാക്കളും ഇരുവശത്തുമുണ്ടാകുക തികച്ചും മാതൃകാപരമാണ്.
ത്രികോണം ABC യില്‍ AB = 12 സെ. മീറ്റര്‍ , കോണ്‍ A = 30 ഡിഗ്രി . AC + BC = 18 സെ. മീറ്റര്‍ . ത്രികോണം നിര്‍മ്മിക്കാമോ? ഉപയോഗിച്ചിരിക്കുന്ന ജ്യാമിതീയ തത്വം എഴുതണം .
ഒന്‍പതാംക്ലാസിലെ അനുപാതം ജ്യാമിതിയില്‍ എന്ന പാഠമാണ് ഇതെഴുതുമ്പോള്‍ മനസില്‍ വരുന്നത് . ഇതിനായി ഒരു വര്‍ക്ക് ഷീറ്റ് തയ്യാറകാകിയിട്ടുണ്ട് . അടുത്ത ദിവസം അത് കൂട്ടിച്ചേര്‍ക്കാം . ഇതിനിടെ ചോദ്യം സ്വയം ചെയ്യാന്‍ കുട്ടികള്‍ക്ക് കൊടുക്കുമല്ലോ?
അര്‍ജുനന്റെ ഉത്തരങ്ങള്‍ക്കായി ഇവിടെ ക്ലിക്ക് ചെയ്യുക
പേജ് ഒന്ന്
പേജ് രണ്ട്
പേജ് മൂന്ന്
പേജ് നാല്
Gazillions
- 8.EE.3. Use numbers expressed in the form of a single digit times a whole-number power of 10 to estimate very large or very small quantities, and to express how many times as much one is than the other. For example, estimate the population of the United States as 3 times 108 and the population of the world as 7 times 109, and determine that the world population is more than 20 times larger.
- 8.EE.4. Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used. Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (e.g., use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology.
My first couple of ideas were: something based on the brilliant scale of the universe applet, or a game looking at different representations of these numbers (my love for rummy games), or an activity based on Fermi problems.
Walking the kids to school this morning I was thinking about the rummy idea, and came up with a new game mechanic variation on rummy: instead of collecting sets, each turn you have to play a card out in front of you. Then opponent can capture that card with a match. Then you could capture the pair with another matching card... kind of a slow run building mechanic. Don't think it will fit for the book, but I will definitely try it in a game later.
Thinking about the matching puzzle, we have:
| Number Names | Measurement Prefixes | Things | Power of Ten |
| One | Humans (meters) | 10^0 | |
| Ten | deca- | Orcas, Anacondas (meters) | 10^1 |
| Hundred | hecto- | Redwood (meters) | 10^2 |
| Thousand | kilo- | Mountains' height (meters), Number of visible stars | 10^3, 10*10*10 |
| Million | mega- | Width of USA (meters) | 10^6 |
| Billion | giga- | Diameter of the Sun (meters), Age of the universe (years) | 10^9 |
| Trillion | tera- | Diameter of the Solar System (meters), US national debt (dollars) | 10^12 |
| Quadrillion | peta- | One light year (meters) | 10^15 |
| Quintillion | exa- | Number of grains of sand on earth | 10^18 |
| Sextillion | zetta- | Diameter of the Milky Way, Number of water molecules in a drop | 10^21 |
| Septillion | yotta- | Diameter of the Universe (meters), Number of stars in the universe | 10^24 |
| Octillion | hella- (petitioned) | Diameter of Universe (mm) Mass of the earth (grams) | 10^27 |
| Nonillion | Number of bacteria on earth | 10^30 | |
| Decillion | Mass of the sun (grams) | 10^33 | |
| Number of atoms in the universe, Volume of the observable universe (m^3) | 10^80 | ||
| Googol | Possible volume of whole universe (m^3) | 10^100 | |
| Centillion | 10^303 | ||
| Googolplex | 10^10^100 |
Why aren't millions called unillions? Or just an Illion? Mil- means 1000! I've always thought it must be because it should be 1000 thousands. Would numbers be more comprehensible without the -illions? The US national debt is 15 thousand thousand thousand thousands!
So the activity for the book could be matching quantities in different columns, though that doesn't give any opportunities for computation. Maybe a bit of a matching puzzle with some clues that require computation and comparison.
I cut things out of my table until it felt a little challenging, with enough structure to serve as an example for deduction and learning. I then put together some clues to help students fill in most, but leave a few for research, deduction or guessing.
The chart on the next page needs to be completed. The researcher has the data to fill in but no idea where to put it. Solve the puzzle of where to put the extra information. There are some blanks in the table, and those are shaded in. However some of the open spaces must get two comparisons, because there are too many for just one in each open space.Unfortunately, these are NOT in order.Names to fill in: Trillion, Quintillion, Centillion, Decillion, Octillion, Nonillion, Quadrillion, and Googol.Prefixes to fill in: yotta, hecto, peta, zetta, mega, and tera.Comparisons to fill in: Possible volume of whole universe (m3), Age of the universe (years), Mountains' height (meters), Width of USA (meters), Anacondas, Diameter of observable universe (mm), Mass of the earth (grams), Number of water molecules in a drop, One light year (meters), Number of bacteria on earth, Number of grains of sand on earth, Diameter of the Solar System (meters), Number of stars in the universe, and Redwood Trees’ height (meters)There were some weird facts the researcher remembered – maybe it will help you fill in the missing information!1. A googolplex has a googol zeroes.2. Thinking about word connections like tricycle and quadrilateral might help.3. The researcher remembers thinking that the number of grains of sand was exallent.4. Number of bacteria on earth is so big that there is about a sextillion for each human. (And there’s billions of humans!)5. A weird science measure is a mole. One mole of water is about 18 g, and has about 602 sextillion atoms.6. It would take about a million earths to have the same mass as the sun, even though the sun is made out of hydrogen and helium, mostly.7. It’s about 2000 km from Michigan to Florida.8. An average grain of sand is about 1mm wide. If you made a line out of all the sand on earth it would stretch for a light year! (The distance light can travel in a year.)9. The biggest official distance measurement is a yottameter, which is a billion times bigger than a petameter.10. In computers, a terabyte (TB) is 1000 GB, and a gigabyte is 1000 MB.
My favorite scientific notation/order of magnitude problems are Fermi problems, so I did put in a few of these for extensions.
Extensions
The brilliant physicist Enrico Fermi used to love posing crazy questions to his students and colleagues, so that now sometimes people call crazy estimation questions ‘Fermi Problems’ in his honor.
For example, he’d ask how many piano tuners there are in Chicago. He’d make a guess as to how many people, how many pianos, how many times they needed tuning and how many pianos one tuner could tune.
Try these Fermi problems and then make up your own! A tip is to think mostly about the powers of ten.1. How many jars of peanut butter to fill up the Empire State Building?
2. How many photographs are in all the houses in your town?
3. How many middle schools are there be in the United States?
4. How many songs are downloaded in Michigan each day?
Dr. Fermi said if you make enough guesses, some are over and some are under, and you would be surprised how accurate you might end up!
Off-topic: 15 October 2011 - World-wide protest day
Was it Cairo or New York, - Occupy Wall Street - where it started? It sure is spreading. I want to express my solidarity with the people out on the streets today in almost 1600 cities world-wide: Occupy Together.
Since the revolution started in Egypt I watched and compared the news from BBC, CNN, Infowars, Al Jazeera, RT ( Russia ), and Press TV ( Iran ). Now Press TV has been taken off-air in the UK. Draw your own conclusions. Here is what Infowars ( US Libertarian ) had to say about it: Press TV taken off air in UK – war for freedom of speech now on.
Now that the alternative media are flourishing, it turns out that we haven't had a free press for decades, Press TV made that painfully clear.
During the last world war, scientists created the atom bomb, period. 'Because they were afraid the Germans would be first.' We have to assure that they don't have an easy excuse like that next time, a free Internet ensures that.
Since the revolution started in Egypt I watched and compared the news from BBC, CNN, Infowars, Al Jazeera, RT ( Russia ), and Press TV ( Iran ). Now Press TV has been taken off-air in the UK. Draw your own conclusions. Here is what Infowars ( US Libertarian ) had to say about it: Press TV taken off air in UK – war for freedom of speech now on.
Now that the alternative media are flourishing, it turns out that we haven't had a free press for decades, Press TV made that painfully clear.
During the last world war, scientists created the atom bomb, period. 'Because they were afraid the Germans would be first.' We have to assure that they don't have an easy excuse like that next time, a free Internet ensures that.
Apakah 4=5 ?
4=5
Buktinya:
-20 = -20
16 - 36 = 25 - 45
4^2 - 9x4 = 5^2 - 9x5
Tambahkan 81/4 di ruas kanan dan kiri
4^2 - 9x4 + 81/4 = 5^ - 9x5 + 81/4
(4 - 9/2)^2 = (5 - 9/2)^2
4 - 9/2 = 5 - 9/2
4 = 5
Buktinya:
-20 = -20
16 - 36 = 25 - 45
4^2 - 9x4 = 5^2 - 9x5
Tambahkan 81/4 di ruas kanan dan kiri
4^2 - 9x4 + 81/4 = 5^ - 9x5 + 81/4
(4 - 9/2)^2 = (5 - 9/2)^2
4 - 9/2 = 5 - 9/2
4 = 5
Jumat, 14 Oktober 2011
Elegi Silaturahim Matematika
Oleh: Marsigit
Matematika1:
Aku adalah matematika. Matematika ya matematika. Aku bukanlah ilmu alam. Tetapi sebetul-betulnya aku adalah ilmu tentang bicara. Guruku adalah Thales.
Matematika2:
Au adalah matematika. Jika aku geometri maka aku bukanlah bilangan. ku ada di dalam pikiranmu. Sesungguhnya sifatku itu abstrak. Yang konkrit itu hanyalah contohku. Aku telah ada secara lengkap dalam
Matematika1:
Aku adalah matematika. Matematika ya matematika. Aku bukanlah ilmu alam. Tetapi sebetul-betulnya aku adalah ilmu tentang bicara. Guruku adalah Thales.
Matematika2:
Au adalah matematika. Jika aku geometri maka aku bukanlah bilangan. ku ada di dalam pikiranmu. Sesungguhnya sifatku itu abstrak. Yang konkrit itu hanyalah contohku. Aku telah ada secara lengkap dalam
Elegi Menyesali Rumahku Yang Terlalu Besar
Oleh Marsigit
Rumah Besar:
Wahai pemilik rumah, kenapa engkau terlihat kurang merawatku. Padahal aku telah engkau bangun dengan biaya yang sangat besar dan melibatkan semua potensimu. Engkau juga tidak membangun rumah ini hanya sendirian. Beberapa generasi sebelummu dan generasimu sekarang juga masih terus terlibat pembangunan rumahmu ini. Bahkan petualangan generasi pendahulumu menjajah
Rumah Besar:
Wahai pemilik rumah, kenapa engkau terlihat kurang merawatku. Padahal aku telah engkau bangun dengan biaya yang sangat besar dan melibatkan semua potensimu. Engkau juga tidak membangun rumah ini hanya sendirian. Beberapa generasi sebelummu dan generasimu sekarang juga masih terus terlibat pembangunan rumahmu ini. Bahkan petualangan generasi pendahulumu menjajah
Elegi Menangkap Anomali
Oleh Marsigit
Dilema:
Pilih mana ya? Diriku atau mereka? Tenaga atau pikiranku? Perasaanku atau faktanya? Hak atau kewajibanku? Terlambat atau hasil yang baik? Tepat waktu tetapi hasil kurang baik? Diam atau bermasalah? Bicara atau juga bermasalah? Tua atau mengaku muda? Muda atau mengaku tua? Punya atau mengaku tidak punya? Tidak punya atau mengaku punya? Berbohong sedikit tetapi selamat? Jujur
Dilema:
Pilih mana ya? Diriku atau mereka? Tenaga atau pikiranku? Perasaanku atau faktanya? Hak atau kewajibanku? Terlambat atau hasil yang baik? Tepat waktu tetapi hasil kurang baik? Diam atau bermasalah? Bicara atau juga bermasalah? Tua atau mengaku muda? Muda atau mengaku tua? Punya atau mengaku tidak punya? Tidak punya atau mengaku punya? Berbohong sedikit tetapi selamat? Jujur
Elegi Pengembaraan Orang Tua Berambut Putih
Oleh Marsigit
Kini aku merasa sudah saatnya aku mengembara. Supaya pengembaraanku bermakna, maka aku akan bertanya kepada para saksi. Tetapi sebelum aku bertanya kepada saksi-saksi terlebih aku ingin sampaikan bahwa sebenar-benar sebenar-benar saksi tidak lain tidak bukan adalah aku sendiri. Aku ingin mengaku bahwa aku mengetahui segala sesuatu, tetapi jika mereka bertanya kepadaku maka dengan
Kini aku merasa sudah saatnya aku mengembara. Supaya pengembaraanku bermakna, maka aku akan bertanya kepada para saksi. Tetapi sebelum aku bertanya kepada saksi-saksi terlebih aku ingin sampaikan bahwa sebenar-benar sebenar-benar saksi tidak lain tidak bukan adalah aku sendiri. Aku ingin mengaku bahwa aku mengetahui segala sesuatu, tetapi jika mereka bertanya kepadaku maka dengan
Elegi Bendungan Komte dan Sungai Positive
Oleh : Marsigit
Sungai transenden:
Aku adalah sungai transenden. Aku mengalirkan air. Air sungaiku bisa mengalir kemana-mana, bisa melewati siapa saja, kapan saja dan dimana saja. Tetapi engkau mungkin tak percaya bahwa aku juga bisa mengalirkan air ke bawah maupun mengalirkan air ke atas. Tetapi selebar-lebar sungaiku adalah pikiran kritismu. Maka sebenar-benar sumber air sungaiku adalah pada
Sungai transenden:
Aku adalah sungai transenden. Aku mengalirkan air. Air sungaiku bisa mengalir kemana-mana, bisa melewati siapa saja, kapan saja dan dimana saja. Tetapi engkau mungkin tak percaya bahwa aku juga bisa mengalirkan air ke bawah maupun mengalirkan air ke atas. Tetapi selebar-lebar sungaiku adalah pikiran kritismu. Maka sebenar-benar sumber air sungaiku adalah pada
Elegi Menggapai Nilai Diri
Oleh Marsigit
Berikut saya nukilkan sebuah pertanyaan dari Sdr ANI ALKHAFI :
Assalamu'alaikum Wr.Wb. Dalam setiap individu itu ada yang mengatakan bahwa manusia dapat menjadikan dirinya terhebat dan mengatakan dirinya termulia, apa itu juga sifat kontradiktif? Bapak yang terhormat, saya ingin tahu bagaimana caranya menjadikan diri kita sebagai perfilsafat (
M381 exam
Did M381 exam. All the questions were doable, easy as a matter of fact. Honestly. I am sure I have full marks for the first question I made. But when I was done and looked at the clock it was already past three o'clock. "Should I have been able to do that question in 10 minutes?", I thought. Maybe. I have a painful ear-infection at the moment, and I was drugged of course, prescription painkillers, doctor's order. And antibiotics, of course. I felt like walking on the moon, in an astronaut's suit. Whatever the outcome may be, I can set it right. More later on the exam, when I feel better.
Kamis, 13 Oktober 2011
ഘനരൂപങ്ങള്‍ - ചോദ്യപേപ്പര്‍
ലേടെക്കിന്റെ വിശാലമായ ക്യാന്‍വാസില്‍ പത്താംക്ലാസിലെ പാഠപുസ്തകം കൃഷ്ണന്‍സാര്‍ തന്റെ ലാപ് ടോപ്പില്‍ ചെയ്തിരുന്നത് ഞാന്‍ കണ്ടിട്ടുണ്ട് . അതില്‍ എന്നെ ഏറ്റവും കൂടുതല്‍ ആകര്‍ഷിച്ചത് ഘനരൂപങ്ങളാണ്. ജീവന്‍ തുടിക്കുന്ന ചിത്രങ്ങളായിരുന്നു അവ. സ്തൂപികയുടെ ഉള്ളിലേയ്ക്ക് നിഴലും വെളിച്ചവും സമ്മേളിച്ചുകൊണ്ട് ത്രിമാനചിത്രങ്ങള്‍ രൂപപ്പെട്ടിരിക്കുന്നകാഴ്ച മനോഹരമാണ്. ലേടെക്കുമായി ഇനിയും ഒത്തിരി ദൂരം യാത്രയുണ്ട്. ഘനരൂപങ്ങളെക്കുറിച്ച് പോസ്റ്റെഴുതവേ സാന്ദര്‍ഭീകമായി പറഞ്ഞതാണ് ഇത്രയും. പാഠപുസ്തകത്തിന്റെ 116-ം മത്തെ പുറം വായിക്കുന്നു. ചതുരപ്പലകകളടുക്കി സമചതുരസ്തൂപികയുടെ ഏകദേശചിത്രം ഉണ്ടാക്കിയതുപോലെ വട്ടപ്പലകകളടുക്കി വൃത്തസ്തൂപികയുടെ ഏകദേശരൂപങ്ങള്‍ ചമയ്ക്കാം. തൊട്ടുപുറകിലെ പേജുകളില്‍ ഇപ്രകാരം നിര്‍മ്മിച്ച സമചതുരസ്തൂപികയുടെ വ്യാപ്തം കാണുന്ന പ്രവര്‍ത്തനം അനുബന്ധമായുണ്ട്. ഈ പ്രവര്‍ത്തനം വൃത്തസ്തൂപികയില്‍ ഒന്നു പ്രയോഗിച്ചുനോക്കാം.വൃത്താകൃതിയില്‍ ധാരാളം കാഡ്ബോര്‍ഡ് കഷങ്ങള്‍ മുറിച്ചെടുക്കുന്നു. അടുത്തടുത്തുള്ള രണ്ട് തകിടുകളുടെ ആരവ്യത്യാസം പരമാവധി കുറവായിരിക്കണം. ഏറ്റവും ചെറിയ വട്ടം ഏറ്റവും മുകളില്‍ വരട്ടെ...
$\mathbf{h}$ ഉയരവും $\mathbf{r}$ആരവുമുള്ള ഒരു വൃത്തചതുരസ്തൂപിക കാണുക.ഇതിനെ മേല്‍പറഞ്ഞപോലെ പരമാവധി കനം കുറച്ച് തകിടുകളാക്കുന്നു. എല്ലാതകിടിനും ഒരേ കനമാണെങ്കില്‍ , ആകെ $\mathbf{n}$ തകിടുകളുണ്ടെങ്കില്‍ ഏറ്റവും മുകളിലെ തകിടിന്റെ ആരം $\frac{\mathbf{r}}{\mathbf{n}}$ആണെന്ന് ഉറപ്പാണല്ലോ?
ഏറ്റവും മുകളിലെ തകിടിന്റെ ആരം $\frac{\mathbf{r}}{\mathbf{n}}$ , അതിനു താഴെയുള്ള തകിടിന്റെ ആരം $\frac{\mathbf{2r}}{\mathbf{n}}$, ആതിനുതാഴെയുള്ള തകിടിന്റെ ആരം $\frac{\mathbf{3r}}{\mathbf{n}}$ എന്നിങ്ങനെ പോകുന്നു. എല്ലാതകിടിന്റെയും ഉയരം $\frac{\mathbf{h}}{\mathbf{n}}$ആകുന്നു.
ഏറ്റവും മുകളിലുള്ള തകിടിന്റെ വ്യാപ്തം $\pi \times (\frac{r}{n})^2 \times \frac{h}{n}$
മുകളില്‍ നിന്നും രണ്ടാമത്തെ തകിടിന്റെ വ്യാപ്തം $\pi \times (\frac{2r}{n})^2 \times \frac{h}{n}$
മുകളില്‍ നിന്നും മൂന്നാമത്തെ തകിടിന്റെ വ്യാപ്തം $ \pi \times (\frac{3r}{n})^2 \times \frac{h}{n}$
അവസാന തകിടിന്റെ വ്യാപ്തം $ \pi \times (\frac{nr}{n})^2 \times \frac{h}{n}$
ഇനി ഈ വ്യാപ്തങ്ങളൊക്കെ കൂട്ടി നോക്കാം. അപ്പോള്‍ വൃത്തസ്തൂപികയുടെ വ്യാപ്തം കിട്ടുമല്ലോ.
വ്യാപ്തം = $\pi\times \frac{ r^2}{6}\times h (1+\frac{1}{n})(2+\frac{1}{n})$
വൃത്തത്തകിടുകളുടെ എണ്ണം പരമാവധി കൂട്ടുക. അതായത് $n$ വില അനന്തമാക്കുകയെന്നൊക്കെ പറയാം .ഇപ്പോള്‍ എന്തു സംഭവിക്കുമെന്ന് ഊഹിക്കാമല്ലോ. $\frac{1}{n}$ എന്നതും $\frac{2}{n}$എന്നതും പൂജ്യത്തോടടുക്കുന്നു. ആകൃതി വൃത്തസ്തൂപികയോടടുക്കുമല്ലോ. അപ്പോള്‍ വൃത്തത്തകിടുകളുടെ എണ്ണം അനന്തമാകുമ്പോഴാണ് ആകൃതി വൃത്തസ്തൂപികയാകുന്നത്. വ്യാപ്തം = $ \frac{1}{3} \pi r^2 h$ ആകുന്നു
സമാന്തരശ്രേണിയില്‍ സൈഡ് ബോക്സില്‍ ആദ്യത്തെ n എണ്ണല്‍സംഖ്യകളുടെ വര്‍ഗ്ഗങ്ങളുടെ തുക $\frac{n(n+1)(2n+1)}{6}$എന്നുതെളിയിച്ചിട്ടുണ്ട്. ഇതിന്റെ ഉപയോഗം ഒരു വൃത്തസ്തൂപികയുടെയും സമചതുരസ്തൂപികയുടെയും വ്യാപ്തം കണക്കാക്കുന്നതിനുള്ള സൂത്രവാക്യം കണ്ടെത്താനാണ്. മറ്റൊരു ഉപയോഗം ഓര്‍ക്കുന്നു..
ചെസ്സ് ബോഡില്‍ എത്ര സമചതുരങ്ങളുണ്ടാകും?
ക്വിസ്സ് മല്‍സരങ്ങളിലെ ഒരു സാധാരണചോദ്യമാണിത് . തിരശ്ചീനമായി എട്ട് $1 \times 1$ സമചതുരങ്ങളുണ്ട് . എതുപോലെ ലംബമായും 8 എണ്ണം ഉണ്ടാകും .ആകെ ഇത്തരം $ 8^2$
തിരശ്ചീനമായി ഏഴ് $2 \times 2 $ സമചതുരങ്ങളും ലംബമായി ഏഴ് $ 2 \times 2 $ സമചതുരങ്ങളും ഉണ്ടാകും .ആകെ $7^2$ എണ്ണം ഉണ്ടാകും
തിരശ്ചീനമായി ആറ് $3 \times 3 $ സമചതുരങ്ങളും ലംബമായി ആറ് $ 3 \times 3$ സമചതുരങ്ങളും ഉണ്ടാകും . എണ്ണം $6^2$
ഇതുപോലെ തുടര്‍ന്നാല്‍ ഒരു $ 8 \times 8$ സമചതുരം ഉണ്ട് . അതാണ് ബോഡ് എണ്ണം $1^2$
ആകെ സമചതുരങ്ങളുടെ എണ്ണം = $\frac{8(8+1)(2 \times 8 +1)}{6}$ = 204
ഘനരൂപങ്ങളില്‍ നിന്നുള്ള ചോദ്യങ്ങള്‍ക്കായി ഇവിടെ ക്ലിക്ക് ചെയ്യുക
Selasa, 11 Oktober 2011
Elegi Mengintip Seminar International Pendidikan Matematika
Ass Wr Wb
Untuk semua Mahasiswa saya S1 dan S2 baik yang sedang mempelajari Filsafat Ilmu, Psikologi Belajar Matematika, Bahasa Inggris untuk Pendidikan Matematika serta Bahasa Inggris untuk Matematika, saya persilahkan untuk mempelajari aspek pelaksanaan Seminar dan Konferensi tentang Pendidikan Matematika, yang akan diselenggarakan di Thailand, 1-6 Nopember 2011, dengan akses ke:
http://
Untuk semua Mahasiswa saya S1 dan S2 baik yang sedang mempelajari Filsafat Ilmu, Psikologi Belajar Matematika, Bahasa Inggris untuk Pendidikan Matematika serta Bahasa Inggris untuk Matematika, saya persilahkan untuk mempelajari aspek pelaksanaan Seminar dan Konferensi tentang Pendidikan Matematika, yang akan diselenggarakan di Thailand, 1-6 Nopember 2011, dengan akses ke:
http://
Senin, 10 Oktober 2011
The book will never die.
A lot has been written about real paper books versus ebooks. Both have their distinct advantages and disadvantages. I have to admit that I read mostly ebooks. They are cheaper and easier to get, store and carry. Mathematics ebooks often have the PDF format. So you need a reader that can handle PDFs. If you use your PC or laptop than a PDF reader is all you need. Most people know Adobe Reader but there are much better programs than Adobe around. With free readers, just like Adobe. My PDF reader of choice is Foxit Reader 5. What I particularly like about Foxit is that it is lightweight, i.e. loads and acts fast. Foxit uses tabbed reading, like internet browsers. If you were in the middle of five books, close Foxit, the program nicely remembers which books you were reading and on what page you left. Most of all, I like the feature that I can highlight what I read. It is almost as if I was reading in a paper book.
Link:
- Foxit Reader 5.
Link:
- Foxit Reader 5.
Minggu, 09 Oktober 2011
Hypercomputation
Only recently lightspeed as the ultimate limit of speed got challenged. It seems they have been challenging the Turing Machine for a while too.
If you start with studying mathematics you are only three or four centuries behind on contemporary mathematics. That's quite a lot of catching up to do. - Some fields started their development in the previous century though. Like mathematical logic, a field I have been studying this year, and have written about so now and then in this blog. Part of mathematical logic is the theory of computation which showed us what can be computed and what can't. That what can be computed is what can be computed on a Turing Machine, period. - That idea is challenged however in the theory of hypercomputation. A new field in mathematics which is trying to go beyond the limits of the Turing Machine.
A book with an overview of the theory is the following.
If you start with studying mathematics you are only three or four centuries behind on contemporary mathematics. That's quite a lot of catching up to do. - Some fields started their development in the previous century though. Like mathematical logic, a field I have been studying this year, and have written about so now and then in this blog. Part of mathematical logic is the theory of computation which showed us what can be computed and what can't. That what can be computed is what can be computed on a Turing Machine, period. - That idea is challenged however in the theory of hypercomputation. A new field in mathematics which is trying to go beyond the limits of the Turing Machine.
A book with an overview of the theory is the following.
Sabtu, 08 Oktober 2011
The mathematics of revolution
The Occupy Wall Street movement is spreading. It reminds me of Conway's Life game. It could spread enormously and still die out soon, or it could cause permanent change without real massive demonstrations. Nobody knows, nobody can predict this. Still, I think it will be very interesting to find mathematical patterns in global, Internet connected, demonstrations like this. I am sure mathematicians of government agencies are working on it.
If a government does not educate even one generation it is lost. It is in their own interest, it is in the interest of the ruling elite to give all citizens a good education. I think that rule fits all political systems. In the US however they use education to enslave people for the rest of their life to the bankers. Paying back student loans turns out to be very difficult. On top of that teachers get fired or are underpaid. - That does not seem right to me.
If a government does not educate even one generation it is lost. It is in their own interest, it is in the interest of the ruling elite to give all citizens a good education. I think that rule fits all political systems. In the US however they use education to enslave people for the rest of their life to the bankers. Paying back student loans turns out to be very difficult. On top of that teachers get fired or are underpaid. - That does not seem right to me.
Langganan:
Postingan (Atom)